
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
分析 ①利用函数奇偶性的定义可判断出?x∈(-1,1),有f(-x)=-f(x),可判断①正确;
②x∈(-1,1),由$f'(x)=\frac{1}{1+x}+\frac{1}{1-x}=\frac{2}{{1-{x^2}}}≥2>0$,可知f(x)在区间(-1,1)上单调递增,可判断②正确;
③利用f′(x)=$\frac{2}{1{-x}^{2}}$在(0,1)单调递增可判断③正确;
④构造函数g(x)=f(x)-2x,则当x∈(0,1)时,g'(x)=f'(x)-2≥0,⇒g(x)在(0,1)单调递增,再利用g(x)=f(x)-2x为奇函数,可判断④正确.
解答 解:对于①,∵f(x)=ln(1+x)-ln(1-x),且其定义域为(-1,1),
∴f(-x)=ln(1-x)-ln(1+x)=-[ln(1+x)-ln(1-x)]=-f(x),
即①?x∈(-1,1),有f(-x)=-f(x),故①是真命题;
对于②,∵x∈(-1,1),由$f'(x)=\frac{1}{1+x}+\frac{1}{1-x}=\frac{2}{{1-{x^2}}}≥2>0$,
可知f(x)在区间(-1,1)上单调递增,
即?x1,x2∈(-1,1)且x1≠x2,有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,故②是真命题;
对于③,∵f′(x)=$\frac{2}{1{-x}^{2}}$在(0,1)单调递增,∴?x1,x2∈(0,1),
有$f(\frac{{{x_1}+{x_2}}}{2})≤\frac{{f({x_1})+f({x_2})}}{2}$,故③是真命题;
对于④,设g(x)=f(x)-2x,则当x∈(0,1)时,g'(x)=f'(x)-2≥0,所以g(x)在(0,1)单调递增,所以当x∈(0,1)时,g(x)>g(0),即f(x)>2x;由奇函数性质可知,?x∈(-1,1),|f(x)|≥2|x|,故④是真命题.
故选:D.
点评 本题考查命题的真假判断与应用,突出考查函数奇偶性与单调性及“凸凹”性的综合应用,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
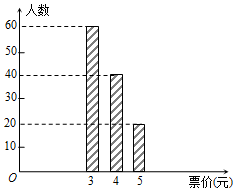 已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{13}$ | D. | $2\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知定直线l:y=x+3,定点A(2,1),以坐标轴为对称轴的椭圆C过点A且与l相切.
已知定直线l:y=x+3,定点A(2,1),以坐标轴为对称轴的椭圆C过点A且与l相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m+n=0 | B. | m-n=0 | C. | mn+1=0 | D. | mn-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com