
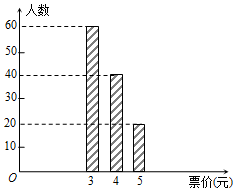
 已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
已知某地铁1号线上,任意一站到M站的票价不超过5元,现从那些只乘坐1号线地铁,且在M站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.分析 (Ⅰ)根据统计图知,计算此人乘坐地铁的票价小于5元的概率;
(Ⅱ)用列举法计算从6人中随机选出2人的票价和恰好为8元的概率.
解答 解:(Ⅰ)记事件A为“此人乘坐地铁的票价小于5元”,…(1分)
由统计图可知,得120人中票价为3元、4元、5元的人数分别为60,40,20(人).
所以票价小于5元的有60+40=100(人),…(2分)
故120人中票价小于5元的频率是$\frac{100}{120}=\frac{5}{6}$,
所以估计此人乘坐地铁的票价小于5元的概率$P(A)=\frac{5}{6}$;…(5分)
(II)记事件B 为“这2人的票价和恰好为8元”,
由统计图,得120人中票价为3元、4元、5元的人数比为60:40:20=3:2:1,
则6名学生中票价为3元、4元、5元的人数分别为3,2,1(人),…(6分)
记票价为3元的同学为a,b,c,票价为4元的同学为d,e,票价为5元的同学为f,
从这6人中随机选出2人,所有可能的选出结果共有15种,它们是:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f).…(8分)
其中事件B的结果有4种,它们是:(a,f),(b,f),(c,f),(d,e),…(10分)
所以这2人的票价和恰好为8元的概率为$P(B)=\frac{4}{15}$.…(12分)
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | 2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -112 | B. | -56 | C. | 112 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3025 | B. | -3024 | C. | 2017 | D. | 9703 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com