
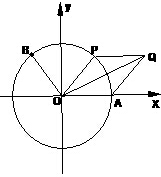
 如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).
如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).分析 (I)直接利用三角函数的定义求出正弦函数以及余弦函数值,即可cosα+sinα的值;
(II)设Pcos2θ,sin2θ,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.表示出表示|$\overrightarrow{OQ}$|,然后通过三角函数的值域求|$\overrightarrow{OQ}$|的最大值.
解答 (本小题13分)
解:(Ⅰ)点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).
可得sinα=$\frac{4}{5}$,cosα=$-\frac{3}{5}$,∴cosα+sinα=$-\frac{3}{5}+\frac{4}{5}=\frac{1}{5}$.
(Ⅱ)因为P(cos2θ,sin2θ),A(1,0)所以$\overrightarrow{OQ}$=$\overrightarrow{OA}+\overrightarrow{OP}$=(1+cos2θ,sin2θ),
所以$\left|\overrightarrow{OQ}\right|$=$\sqrt{(1+cos2θ)^{2}+{sin}^{2}2θ}$=$\sqrt{2+2cos2θ}$=2|cosθ|,因为$\frac{π}{6}≤θ≤\frac{π}{2}$,
所以$\left|\overrightarrow{OQ}\right|$=2|cosθ|∈$[0,\sqrt{3}]$,
|$\overrightarrow{OQ}$|的最大值$\sqrt{3}$.
点评 本题考查三角函数的定义的应用,三角函数最值的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
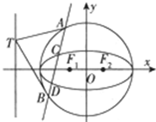 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com