
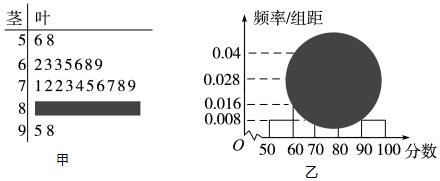
分析 (1)利用茎叶图和频率分布直方图确定分数在[50,60)的面积,然后求出对应的频率和人数.
(2)利用茎叶图计算出分数在[80,90)之间的人数,以及对应的频率,然后计算出对应矩形的高.
(3)利用平均数的定义即可求出.
解答 解:(1)由茎叶图知,分数在[50,60)之间的频数为2,
由频率分布直方图知,分数在[50,60)之间的频率为0.008×10=0.08,
所以该班全体男生人数为$\frac{2}{0.08}=25$(人)
(2)由茎叶图可见部分共有21人,所以[80,90)之间的男生人数为25-21=4(人),
所以,分数在[80,90)之间的频率为$\frac{4}{25}=0.16$,
频率分布直方图中[80,90)间的矩形的高为$\frac{0.16}{10}=0.016$.
(3)由频率分布直方图可知,所求该班全体男生的数学平均成绩约为$\overline x=({0.008×55+0.028×65+0.04×75+0.016×85+0.008×95})×10=73.8$
点评 本题主要考查茎叶图和频率分布直方图的识别和应用,比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,10) | B. | (1,9) | C. | (0,9) | D. | (9,11) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
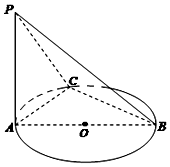 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
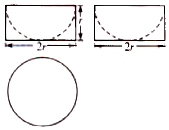 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com