
分析 (1)由已知条件可得$\left\{\begin{array}{l}{{a}^{2}-1=0}\\{a-1≠0}\end{array}\right.$求解得a的值;
(2)由(1)可得z1=1,再求出|z2|,结合已知条件可得$\sqrt{{m}^{2}+(m-1)^{2}}>1$,求解可得答案.
解答 解:(1)∵复数z1是实数,∴$\left\{\begin{array}{l}{{a}^{2}-1=0}\\{a-1≠0}\end{array}\right.$,解得a=-1;
(2)由(1)可得z1=1,
∵$|{z}_{2}|=\sqrt{{m}^{2}+(m-1)^{2}}$,
又|z1|<|z2|,∴$\sqrt{{m}^{2}+(m-1)^{2}}>1$,解得m<0或m>1.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,内角A,B,C所对的边分别为a,b,c且2a cosC-c=2b.
在△ABC中,内角A,B,C所对的边分别为a,b,c且2a cosC-c=2b.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•e-x+1 | C. | y=f(x)•e-x-1 | D. | y=f(x)•ex+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
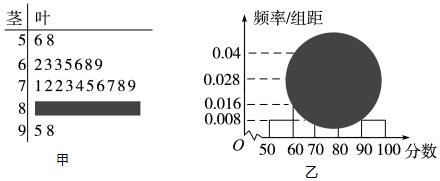
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com