
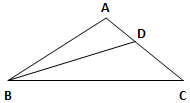
 在△ABC中,内角A,B,C所对的边分别为a,b,c且2a cosC-c=2b.
在△ABC中,内角A,B,C所对的边分别为a,b,c且2a cosC-c=2b.分析 (Ⅰ)根据正弦定理和两角和的正弦公式即可得到cosA=-$\frac{1}{2}$,问题得以解决,
(Ⅱ)根据正弦定理和余弦定理即可求出答案.
解答 解:(Ⅰ)2acosC-c=2b⇒2sinAcosC-sinC=2sinB,
2sinAcosC-sinC=2sin(A+C)=2sinAcosC+2cosAsinC⇒-sinC=2cosAsinC,
∵sinC≠0,
∴$cosA=-\frac{1}{2}$,
而A∈(0,π),
∴$A=\frac{2π}{3}$;
(Ⅱ)在△ABD中,由正弦定理得,$\frac{AB}{sin∠ADB}=\frac{BD}{sinA}⇒sin∠ADB=\frac{AB•sinA}{BD}=\frac{{\sqrt{2}}}{2}$
∴$∠ADB=\frac{π}{4}$,
∴$∠ABC=\frac{π}{6},∠ACB=\frac{π}{6},AC=AB=\sqrt{2}$
由余弦定理,$a=BC=\sqrt{A{B^2}+A{C^2}-2AB•AC•cosA}=\sqrt{6}$.
点评 本题考查了正弦定理和余弦定理和两角和正弦公式,考查了学生的运算能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | ?p:有的三角形不是等腰三角形 | |
| B. | ?p:有的三角形是不等腰三角形 | |
| C. | ?p:所有的三角形都不是等腰三角形 | |
| D. | ?p:所有的三角形都是等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
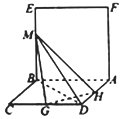 如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com