
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•e-x+1 | C. | y=f(x)•e-x-1 | D. | y=f(x)•ex+1 |
分析 根据f(x)是奇函数可得f(-x)=-f(x),因为x0是y=f(x)-ex的一个零点,代入得到一个等式,利用这个等式对A、B、C、D四个选项进行一一判断.
解答 解:f(x)是奇函数,∴f(-x)=-f(x)
且x0是y=f(x)-ex的一个零点,∴f(x0)-ex0=0,∴f(x0)=ex0,
把-x0分别代入下面四个选项,
A、y=f(x0)ex0-1=ex0ex0-1≠0,故A错误;
B、y=f(-x0)ex0+1=-(ex0)2+1≠0,故B错误;
C、y=ex0f(-x0)-1=-ex0•ex0-1≠0,故C不正确;
D、y=e-x0f(-x0)+1=-ex0e-x0+1=0,故D正确.
故选:D.
点评 此题主要考查函数的零点问题以及奇函数的性质,此题是一道中档题,需要一一验证.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
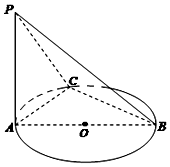 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com