
(本小题满分10分)选修4—1:几何证明选讲
如图所示, 为圆
为圆 的切线,
的切线, 为切点,
为切点,
 ,
,
 的角平分线与
的角平分线与 和圆
和圆 分别交于点
分别交于点 和
和 .
.

(1)求证
(2)求 的值.
的值.
(1)证明见解析;(2)360.
【解析】
试题分析:(1)从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线,平分两条切线的夹角;(2)判断三角形相似:一是平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似;二是如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似;三是如果两个三角形的两组对应边的比相等,并且相应的夹角相等, 那么这两个三角形相似;四是如果两个三角形的三组对应边的比相等,那么这两个三角形相似;五是对应角相等,对应边成比例的两个三角形叫做相似三角;(3)切割线定理:切割线定理,是圆幂定理的一种,从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
试题解析:(1)∵ 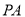 为圆
为圆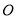 的切线,
的切线, 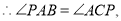 又
又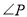 为公共角,
为公共角,
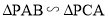
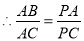 . 4分
. 4分
(2)∵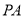 为圆
为圆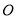 的切线,
的切线,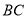 是过点
是过点 的割线,
的割线, 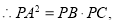

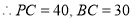 又∵
又∵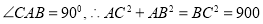
又由(1)知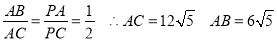 ,
,
连接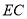 ,则
,则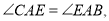
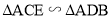 ,则
,则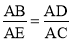 ,
,
∴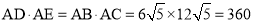 . 10分
. 10分
考点:1、切割线定理的应用;2、三角形相似的应用.
考点分析: 考点1:几何证明选讲 试题属性

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源:2014-2015学年广东省汕头市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知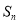 是数列
是数列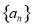 的前
的前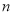 项和,且满足
项和,且满足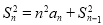 (
(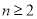 ,
,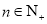 ),又已知
),又已知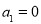 ,
,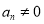 ,
, ,
,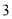 ,
,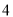 ,
, .
.
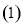 计算
计算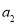 ,
,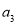 ,并求数列
,并求数列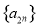 的通项公式;
的通项公式;
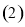 若
若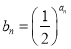 ,
,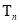 为数列
为数列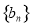 的前
的前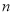 项和,求证:
项和,求证: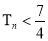 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省兰州市高三诊断考试理科数学试卷(解析版) 题型:选择题
在直角坐标系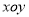 中,设
中,设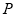 是曲线
是曲线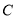 :
: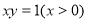 上任意一点,
上任意一点,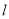 是曲线
是曲线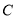 在点
在点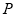 处的切线,且
处的切线,且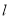 交坐标轴于
交坐标轴于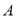 ,
,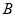 两点,则以下结论正确的是
两点,则以下结论正确的是
A.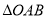 的面积为定值
的面积为定值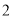
B.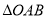 的面积有最小值为
的面积有最小值为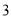
C.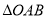 的面积有最大值为
的面积有最大值为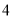
D.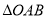 的面积的取值范围是
的面积的取值范围是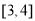
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考文科数学试卷(解析版) 题型:选择题
定义行列式运算: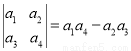 .若将函数
.若将函数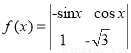 的图象向左平移
的图象向左平移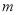
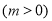 个单位后,所得图象对应的函数为奇函数,则
个单位后,所得图象对应的函数为奇函数,则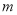 的最小值是( )
的最小值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查理科数学试卷(解析版) 题型:解答题
(本小题满分7分)选修4-2:矩阵与变换
已知二阶矩阵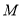 有特征值λ1=4及属于特征值4的一个特征向量
有特征值λ1=4及属于特征值4的一个特征向量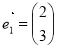 并有特征值
并有特征值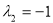 及属于特征值-1的一个特征向量
及属于特征值-1的一个特征向量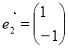 ,
, 
(Ⅰ )求矩阵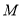 ;(Ⅱ )求
;(Ⅱ )求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com