
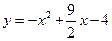 ,通过原点O作C的切线
,通过原点O作C的切线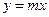 ,使切点P在第一象限.
,使切点P在第一象限. 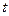 ,为使DOPQ的面积小于DPQR的面积,试求
,为使DOPQ的面积小于DPQR的面积,试求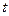 的取值范围.
的取值范围. ,P的坐标为(2,1)
,P的坐标为(2,1) ,-4)
,-4) 范围为t<
范围为t<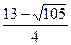 或t>
或t>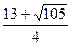 .
.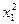 +
+ x1 – 4……②,
x1 – 4……②,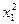 +(k–
+(k– )x1+4=0………
)x1+4=0………
 …………………………………………2分
…………………………………………2分 )2–16=0,得:k=
)2–16=0,得:k= 或k=
或k= ……………………4分
……………………4分 时x1= -2,y1= -1
时x1= -2,y1= -1 7;当k=
7;当k= 时,x1= 2,y1= 1;
时,x1= 2,y1= 1; ,P的坐标为(2,1),……………6分
,P的坐标为(2,1),……………6分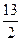 x+9=0,设Q点的坐标为(x2, y2),则2x2=9,所以x2=
x+9=0,设Q点的坐标为(x2, y2),则2x2=9,所以x2= ,y2=-4,
,y2=-4, ,-4),………………………
,-4),……………………… ………
……… ………………10分
………………10分 t–4),它到直线PQ的距离为:
t–4),它到直线PQ的距离为: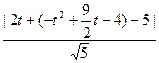 =
=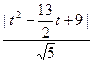 ……………………………………12分
……………………………………12分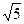 ,SDOPQ=
,SDOPQ= ´PQ´OP,SDPQR=
´PQ´OP,SDPQR= ´PQ´d,
´PQ´d, 即:
即: OP < d,即:
OP < d,即: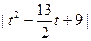 >5,……………………………………14分
>5,……………………………………14分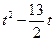 +4>0或
+4>0或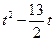 +14<0
+14<0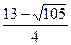 或t>
或t>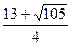
 范围为t<
范围为t<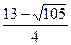 或t>
或t>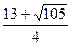 .……………………………16分
.……………………………16分

科目:高中数学 来源:不详 题型:解答题
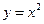 和三个点
和三个点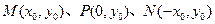
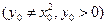 ,过点
,过点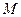 的一条直线交抛物线于
的一条直线交抛物线于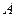 、
、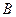 两点,
两点,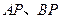 的延长线分别交曲线
的延长线分别交曲线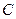 于
于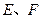 .
.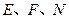 三点共线;
三点共线;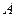 、
、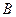 、
、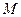 、
、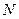 四点共线,问:是否存在
四点共线,问:是否存在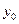 ,使以线段
,使以线段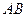 为直径的圆与抛物线有异于
为直径的圆与抛物线有异于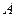 、
、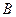 的交点?如果存在,求出
的交点?如果存在,求出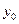 的取值范围,并求出该交点到直线
的取值范围,并求出该交点到直线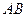 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.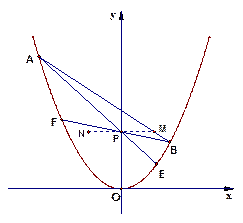
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com