
【题目】凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1 , x2 , …,xn , 有 ![]() ≤f(
≤f( ![]() ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=x3+3x2﹣mx+1在[﹣2,2]上为单调增函数,则实数m的取值范围为( )
A.m≤﹣3
B.m≤0
C.m≥﹣24
D.m≥﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为检验寒假学生自主学习的效果,年级部对某班50名学生各科的检测成绩进行了统计,下面是政治成绩的频率分布直方图,其中成绩分组区间是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求图中的![]() 值及平均成绩;
值及平均成绩;
(2)从分数在![]() 中选5人记为
中选5人记为![]() ,从分数在
,从分数在![]() 中选3人,记为
中选3人,记为![]() ,8人组成一个学习小组.现从这5人和3人中各选1人做为组长,求
,8人组成一个学习小组.现从这5人和3人中各选1人做为组长,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-4:坐标系与参数方程
已知直线的极坐标方程为![]() ,圆
,圆![]() 的参数方程为
的参数方程为
![]() (其中
(其中![]() 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆![]() 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年前五个月每月生产某种产品的数量C(件)关于时间t(月)的函数图象如图所示,则这个工厂对这种产品来说( )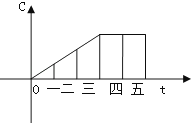
A.一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少
B.一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平
C.一至三月每月生产数量逐月增加,四、五两月均停止生产
D.一至三月每月生产数量不变,四、五两月均停止生产
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的二项展开式中所有奇数项的系数之和为512,
的二项展开式中所有奇数项的系数之和为512,
(1)求展开式的所有有理项(指数为整数).
(2)求(1﹣x)3+(1﹣x)4+…+(1﹣x)n展开式中x2项的系数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1﹣x).
(1)在如图所给直角坐标系中画出函数f(x)的草图,并直接写出函数f(x)的零点;
(2)求出函数f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 为参数
为参数![]() 和直线
和直线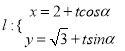
![]() 其中
其中![]() 为参数,
为参数, ![]() 为直线
为直线![]() 的倾斜角
的倾斜角![]() .
.
(1)当![]() 时,求圆上的点到直线
时,求圆上的点到直线![]() 的距离的最小值;
的距离的最小值;
(2)当直线![]() 与圆
与圆![]() 有公共点时,求
有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com