
分析 (1)由已知,利用正弦定理化简可得cosC=$\frac{1}{2}$,根据特殊角的三角函数值即可求C的值.
(2)利用三角函数恒等变换的应用化简所求为$sin(2B+\frac{π}{6})+\frac{1}{2}$,结合范围B∈($\frac{π}{6}$,$\frac{π}{2}$),利用正弦函数的图象和性质即可求解范围.
解答 (本小题满分12分)
解:(1)∵由已知,2sinBsinCcosC=sinCsinB,
∴cosC=$\frac{1}{2}$,
∴可得:C=$\frac{π}{3}$,
(2)∵$\sqrt{3}sinBcosB+{cos^2}B$=$\frac{{\sqrt{3}}}{2}sin2B+\frac{1+cos2B}{2}$=$sin(2B+\frac{π}{6})+\frac{1}{2}$,
又∵△ABC为锐角三角形,且$C=\frac{π}{3}$,
∴B∈($\frac{π}{6}$,$\frac{π}{2}$),可得:2B+$\frac{π}{6}$∈($\frac{π}{2}$,$\frac{7π}{6}$),
∴sin(2B+$\frac{π}{6}$)+$\frac{1}{2}$∈(0,$\frac{3}{2}$).
点评 本题主要考查了正弦定理,特殊角的三角函数值,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的综合应用,考查了转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
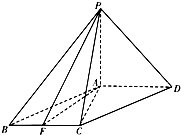 如图四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是平行四边形,∠ACB=90°,AB=$\sqrt{2}$,PA=BC=1,F是BC的中点.
如图四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是平行四边形,∠ACB=90°,AB=$\sqrt{2}$,PA=BC=1,F是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±2 | C. | ±$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com