
分析 (Ⅰ)由已知得${a}_{n}={{a}_{n-1}+(-1)}^{n}+n$,∴${a}_{n}={a}_{n-2}+(-1)^{n-1}+n-1$,当n为奇数时,an=an-2+n,累加,得an=$\frac{(n+1)^{2}}{4}$;当n为偶数时,an=an-2+n-2,累加,得an=$\frac{{n}^{2}-2n+8}{4}$,由此能求出{an}的通项公式.
(Ⅱ)$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{2n}}$=($\frac{1}{{a}_{1}}+\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{2n-1}}$)+($\frac{1}{{a}_{2}}+\frac{1}{{a}_{4}}+…+\frac{1}{{a}_{2n}}$)=4($\frac{1}{{2}^{2}}+\frac{1}{{4}^{2}}+…+\frac{1}{(2n)^{2}}$)+4($\frac{1}{8}+\frac{1}{16}+…+\frac{1}{4{n}^{2}-4n+8}$),由此利用放缩法能证明$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2n}}}}<\frac{7}{2}$.
解答 解:(Ⅰ)∵数列{an},满足a1=b1=1,an+1=bn+n,${b_{n+1}}={a_n}+{({-1})^{n+1}}$,
∴${a}_{n}={{a}_{n-1}+(-1)}^{n}+n$,∴${a}_{n}={a}_{n-2}+(-1)^{n-1}+n-1$,
当n为奇数时,an=an-2+n,累加,得:${a}_{n}={a}_{1}+\frac{n+3}{2}•\frac{n-1}{2}$=$\frac{(n+1)^{2}}{4}$,
当n为偶数时,an=an-2+n-2,累加,得${a}_{n}={a}_{2}+\frac{n-2}{2}•\frac{n}{2}$=$\frac{{n}^{2}-2n+8}{4}$,
故{an}的通项公式为an=$\left\{\begin{array}{l}{\frac{(n+1)^{2}}{4},n为奇数}\\{\frac{{n}^{2}-2n+8}{4},n为偶数}\end{array}\right.$,(n∈N*).
证明:(Ⅱ)$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{2n}}$=($\frac{1}{{a}_{1}}+\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{2n-1}}$)+($\frac{1}{{a}_{2}}+\frac{1}{{a}_{4}}+…+\frac{1}{{a}_{2n}}$)
=4($\frac{1}{{2}^{2}}+\frac{1}{{4}^{2}}+…+\frac{1}{(2n)^{2}}$)+4($\frac{1}{8}+\frac{1}{16}+…+\frac{1}{4{n}^{2}-4n+8}$)
<4($\frac{1}{1×3}+\frac{1}{3×5}+…+\frac{1}{(2n-1)×(2n+1)}$)+($\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{n}^{2}-n+2}$)
<2[(1-$\frac{1}{3}$)+($\frac{1}{3}-\frac{1}{5}$)+…+($\frac{1}{2n-1}-\frac{1}{2n+1}$)]+[$\frac{1}{2}+(1-\frac{1}{2})+…+(\frac{1}{n-1}-\frac{1}{n})$]
=2(1-$\frac{1}{2n+1}$)+($\frac{3}{2}$-$\frac{1}{n}$)<2+$\frac{3}{2}$=$\frac{7}{2}$.
故$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2n}}}}<\frac{7}{2}$.
点评 本题考查数列的通项公式的求法,考查数列不等式的证明,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想,考查创新意识、应用意识,是中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
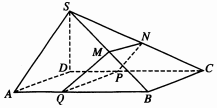 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于P,Q两点(不与A,B重合).
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于P,Q两点(不与A,B重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com