
设数列{an}的前n项和为Sn,且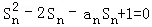 ,n=1,2,3
,n=1,2,3
(1)求a1,a2;
(2)求Sn与Sn﹣1(n≥2)的关系式,并证明数列{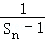 }是等差数列;
}是等差数列;
(3)求S1•S2•S3 S2011•S2012的值.
(1) ,
,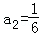 ;(2)SnSn﹣1﹣2Sn+1=0;(3)
;(2)SnSn﹣1﹣2Sn+1=0;(3)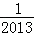 .
.
解析试题分析:(1)直接利用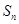 与
与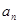 的关系式求
的关系式求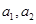 的值;(2)当
的值;(2)当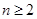 时,把
时,把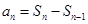 代入已知关系式可得与
代入已知关系式可得与 的关系式,再由此关系式,去凑出
的关系式,再由此关系式,去凑出 和
和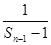 ,可得所求数列
,可得所求数列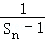 是等差数列,进而得通项
是等差数列,进而得通项 的表达式,从而得
的表达式,从而得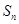 的表达式;(3)由(2)中
的表达式;(3)由(2)中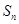 的表达式易求S1•S2•S3 S2011•S2012的值.
的表达式易求S1•S2•S3 S2011•S2012的值.
试题解析:(1)解:当n=1时,由已知得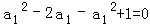 ,解得
,解得 ,
,
同理,可解得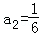 . (4分)
. (4分)
(2)证明:由题设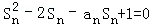 ,
,
当n≥2时,an=Sn﹣Sn﹣1,代入上式,得SnSn﹣1﹣2Sn+1=0,
∴ , (7分)
, (7分)
∴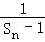 =﹣1+
=﹣1+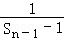 ,
,
∴{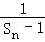 }是首项为
}是首项为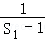 =﹣2,公差为﹣1的等差数列, (10分)
=﹣2,公差为﹣1的等差数列, (10分)
∴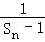 =﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=
=﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=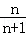 . (12分)
. (12分)
(3)解:S1•S2•S3 S2011•S2012= •
•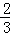 •
•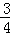 •
•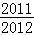 •
•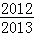 =
=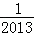 . (14分)
. (14分)
考点:1、等差数列;2、数列的前n项和与通项的综合应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
若无穷数列 满足:①对任意
满足:①对任意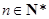 ,
,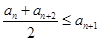 ;②存在常数
;②存在常数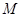 ,对任意
,对任意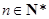 ,
,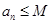 ,则称数列
,则称数列 为“
为“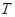 数列”.
数列”.
(Ⅰ)若数列 的通项为
的通项为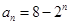
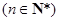 ,证明:数列
,证明:数列 为“
为“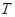 数列”;
数列”;
(Ⅱ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“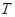 数列”,证明:对任意
数列”,证明:对任意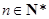 ,
,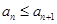 ;
;
(Ⅲ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“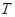 数列”,证明:存在
数列”,证明:存在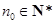 ,数列
,数列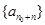 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列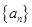 的通项公式为
的通项公式为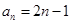 ,数列
,数列 的前
的前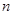 项和为
项和为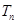 ,且满足
,且满足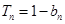 .
.
(1)求 的通项公式;
的通项公式;
(2)在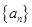 中是否存在使得
中是否存在使得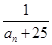 是
是 中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
等差数列{am}的前m项和为Sm,已知S3= ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,
(1)求数列{am}的通项公式.
(2)若{am}又是等比数列,令bm= ,求数列{bm}的前m项和Tm.
,求数列{bm}的前m项和Tm.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列 的各项均为正数,
的各项均为正数,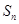 为其前
为其前 项和,对于任意的
项和,对于任意的 ,总有
,总有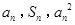 成等差数列.
成等差数列.
(1)求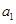 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)设数列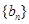 的前
的前 项和为
项和为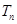 ,且
,且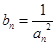 ,求证:对任意正整数
,求证:对任意正整数 ,总有
,总有
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
四川省广元市2008年新建住房400万平方米,其中有250万平方米是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2008年为累计的第一年)将首次不少于4 750万平方米?
(2)到2013年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%吗?为什么
(参考数据:1.084≈1.36,1.085≈1.47,1.086≈1.59)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com