
已知函数f(x)=ax+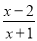 (a>1).
(a>1).
(1)证明:函数f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根.
(1)见解析 (2)见解析
【解析】证明:(1)任取x1,x2∈(-1,+∞),不妨设x1<x2,
由于a>1,ax1<ax2,∴ax2-ax1>0.
又∵x1+1>0,x2+1>0,
∴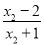 -
-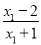
=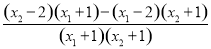
=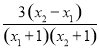 >0,
>0,
于是f(x2)-f(x1)=ax2-ax1+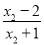 -
-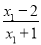 >0,
>0,
即f(x2)>f(x1),
故函数f(x)在(-1,+∞)上为增函数.
(2)证法一:假设存在x0<0(x0≠-1)满足f(x0)=0,
则ax0=-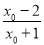 .
.
∵a>1,
∴0<ax0<1.
∴0<-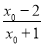 <1,即
<1,即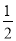 <x0<2,与假设x0<0相矛盾,
<x0<2,与假设x0<0相矛盾,
故方程f(x)=0没有负数根.
证法二:假设存在 x0<0(x0≠-1)满足f(x0)=0,
①若-1<x0<0,
则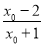 <-2,0<ax0<1,
<-2,0<ax0<1,
∴f(x0)<-1,与f(x0)=0矛盾.
②若x0<-1,则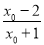 >0,1>ax0>0,
>0,1>ax0>0,
∴f(x0)>0,与f(x0)=0矛盾,
故方程f(x)=0没有负数根.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:填空题
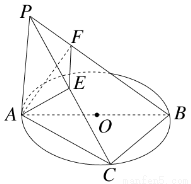
如图PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:选择题
某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为( )
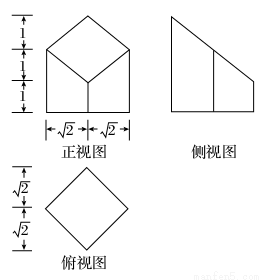
A.4 B.2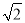 C. D.8
C. D.8
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:填空题
用数学归纳法证明不等式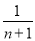 +
+ +…+
+…+ >
> 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:选择题
用数学归纳法证明1+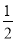 +
+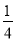 +…+
+…+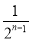 >
>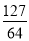 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:选择题
用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个偶数”正确的反设为( )
A.a,b,c中至少有两个偶数
B.a,b,c中至少有两个偶数或都是奇数
C.a,b,c都是奇数
D.a,b,c都是偶数
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:填空题
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2,第3行第1个数字为4,…)是________;(2)第63行从左至右的第4个数字应是________.
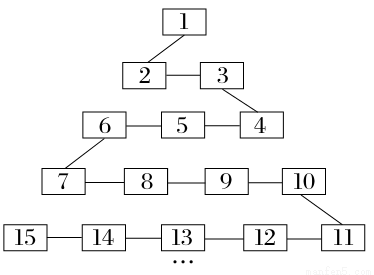
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:解答题
已知A、B、C是平面上任意三点,BC=a,CA=b,AB=c,求y=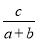 +
+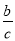 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
已知m>1,a=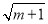 -
- ,b=
,b=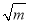 -
-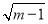 ,则以下结论正确的是( )
,则以下结论正确的是( )
A.a>b B.a=b
C.a<b D.a,b的大小不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com