练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

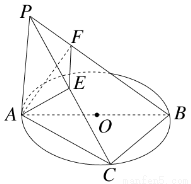
    如图PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC，其中真命题的序号是________．

     

     

    ①②④

    【解析】①AE?平面PAC，BC⊥AC，BC⊥PA⇒AE⊥BC，

    故①正确，②AE⊥PB，AF⊥PB⇒EF⊥PB，故②正确，③若AF⊥BC⇒AF⊥平面PBC，则AF∥AE与已知矛盾，故③错误，由①可知④正确．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-3圆的方程（解析版） 题型：选择题

    过点M(1,2)的直线l将圆(x－2)2＋y2＝9分成两段弧，当其中的劣弧最短时，直线的方程是(　　)

    A．x＝1 B．y＝1

    C．x－y＋1＝0 D．x－2y＋3＝0

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-7立体几何中的向量方法（解析版） 题型：解答题

    如图，在直三棱柱A1B1C1－ABC中，AB⊥AC，AB＝AC＝2，A1A＝4，点D是BC的中点．

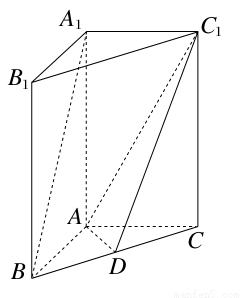
    (1)求异面直线A1B与C1D所成角的余弦值；

    (2)求平面ADC1与平面ABA1夹角的正弦值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-6空间向量及运算（解析版） 题型：选择题

    若向量a＝(1,1，x)，b＝(1,2,1)，c＝(1,1,1)，满足条件(c－a)·(2b)＝－2，则x＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-5直线、平面垂直的判定及性质（解析版） 题型：解答题

    如图所示，在四棱锥P－ABCD中，四边形ABCD为菱形，△PAD为等边三角形，平面PAD⊥平面ABCD，且∠DAB＝60°，AB＝2，E为AD的中点．

    (1)求证：AD⊥PB；

    (2)求点E到平面PBC的距离．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-5直线、平面垂直的判定及性质（解析版） 题型：选择题

    如图(a)，在正方形ABCD中，E、F分别是BC、CD的中点，G是EF的中点，现在沿AE、AF及EF把这个正方形折成一个四面体，使B、C、D三点重合，重合后的点记为H，如图(b)所示，那么，在四面体A－EFH中必有(　　)

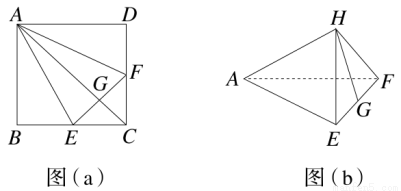
    A．AH⊥△EFH所在平面

    B．AG⊥△EFH所在平面

    C．HF⊥△AEF所在平面

    D．HG⊥△AEF所在平面

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-4直线、平面平行的判定及性质（解析版） 题型：解答题

    如图，在正三棱柱ABC－A1B1C1中，点D为棱AB的中点，BC＝1，AA1＝.

    (1)求证：BC1∥平面A1CD；

    (2)求三棱锥D－A1B1C的体积.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：填空题

    如图所示为棱长是1的正方体的表面展开图，在原正方体中，给出下列三个结论：

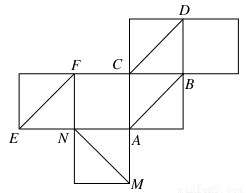
    ①点M到AB的距离为；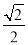

    ②三棱锥C－DNE的体积是；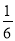

    ③AB与EF所成的角是.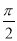

    其中正确结论的序号是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：解答题

    已知函数f(x)＝ax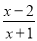＋ (a>1)．

    (1)证明：函数f(x)在(－1，＋∞)上为增函数；

    (2)用反证法证明方程f(x)＝0没有负数根．

     

    查看答案和解析>>

    同步练习册答案