已知数列{an} 的前n项和Sn=2n2+2n,数列{bn} 的前n项和Tn=2-bn.
(1)求数列{an} 与{bn} 的通项公式;
(2)设cn=an2•bn,求数列{cn}的最大值.
解:(1)由于a
1=S
1=4
当n≥2时,a
n=S
n-S
n-1=(2n
2+2n)-[2(n-1)
2+2(n-1)]=4n,
∴a
n=4n,n∈N
*,
又当n≥2时b
n=T
n-T
n-1=(2-b
n)-(2-b
n-1),∴2b
n=b
n-1∴数列b
n是等比数列,其首项为1,公比为

,∴b
n=(

)
n-1.
(2)由(1)知C
1=a
12b
n=16n
2(

)
n-1,

=
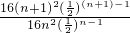
=

.
由

<1得

<1,解得n≥3.
又n≥3时,

<1成立,即

<1,由于c
n>0恒成立.
因此,当且仅当n≥3时c
n+1<c
n.C
1=16,C
2=32,C
3=38,
所以数列{c
n}的最大值38.
分析:(1)由题意求出a
1=4,利用a
n=S
n-S
n-1化简可得,a
n=4n,n∈N
*,再由b
n=T
n-T
n-1,可得2b
n=b
n-1说明数列{b
n}是等比数列,由此可求数列{b
n}的通项公式.
(2)由题意c
n=a
n2•b
n,推出

的取值范围,由此判断数列满足c
n+1<c
n.进而可求出数列{c
n}的最大值.
点评:由a
n=S
n-S
n-1可求出b
n和a
n,这是数列中求通项的常用方法之一,在求出b
n和a
n后,进而得到c
n,接下来用作差法来比较大小,这也是一常用方法.考查计算能力.

 ,∴bn=(
,∴bn=( )n-1.
)n-1. )n-1,
)n-1, =
=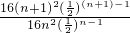 =
= .
. <1得
<1得 <1,解得n≥3.
<1,解得n≥3. <1成立,即
<1成立,即 <1,由于cn>0恒成立.
<1,由于cn>0恒成立. 的取值范围,由此判断数列满足cn+1<cn.进而可求出数列{cn}的最大值.
的取值范围,由此判断数列满足cn+1<cn.进而可求出数列{cn}的最大值.
