
分析 (1)根据公式an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$计算an;
(2)使用裂项法求和.
解答 解:(1)当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=$\frac{3{n}^{2}-n}{2}$-$\frac{3(n-1)^{2}-(n-1)}{2}$=3n-2,
经检验,当n=1时,上式仍成立,
∴an=3n-2.
(2)bn=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}$($\frac{1}{3n-2}-\frac{1}{3n+1}$).
∴Tn=$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}-\frac{1}{10}$+…+$\frac{1}{3n-2}-\frac{1}{3n+1}$)
=$\frac{1}{3}$(1-$\frac{1}{3n+1}$)
=$\frac{n}{3n+1}$.
点评 本题考查了数列通项公式的求法,裂项法数列求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x2+(y+1)2=1 | B. | x2+(y-1)2=1 | C. | (x-1)2+(y-1)2=1 | D. | x2+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
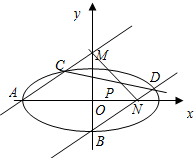 如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.
如图,分别过椭圆L的左顶点A(-3,0)和下顶点B且斜率为k(k>0)的两条直线l1和l2分别交椭圆L于点C,D,且l1交y轴于点M,l2交x轴于点N,且线段CD与线段MN相交于点P.当k=3时,△ABM是直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1]∪(2,+∞) | B. | [0,1)∪(2,+∞) | C. | (-∞,1] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_3^3$•$A_4^3$ | B. | $A_3^3$•$A_3^3$ | C. | $A_4^3$•$A_4^3$ | D. | 2$A_3^3$•$A_3^3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$x | B. | $\frac{5}{6}\root{6}{x}$ | C. | $\frac{5}{{6\root{6}{x}}}$ | D. | $\frac{{5\root{6}{x}}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com