
| רҵ�γɼ�xi���֣� | 7 | 7 | 8 | 9 | 9 |
| ��нyi����Ԫ�� | 10 | 12 | 14 | 14 | 15 |
���� ��1�����ݱ������ݣ�����$\overline{x}$��$\overline{y}$�����ù�ʽ����������ϵ��r��
��2��������Իع鷽�̣����ûع鷽�̼���x=9.6ʱ$\stackrel{��}{y}$��ֵ���ɣ�
��3�����û����¼����ı���ŵ���͵ĸ���ֵ���ɣ�
��� �⣺��1�����ݱ������ݣ�����$\overline{x}$=$\frac{1}{5}$����7+7+8+9+9��=8��
$\overline{y}$=$\frac{1}{5}$����10+12+14+14+15��=13��
$\underset{\stackrel{5}{��}}{i=1}$xiyi-5$\overline{x}$$\overline{y}$=��7��10+7��12+8��14+9��14+9��15��-5��8��13=7��
$\underset{\stackrel{5}{��}}{i=1}$${{x}_{i}}^{2}$-5${\overline{x}}^{2}$=��72+72+82+92+92��-5��82=4��
$\underset{\stackrel{5}{��}}{i=1}$${{y}_{i}}^{2}$-5${\overline{y}}^{2}$=��102+122+142+142+152��-5��132=16��
����רҵ�γɼ�����н���������ϵ��Ϊ��
r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}•\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n{\overline{y}}^{2}}}$=$\frac{7}{\sqrt{4}��\sqrt{16}}$=$\frac{7}{8}$��
��2����רҵ�γɼ�����н��ϵ�����Իع鷽��Ϊ$\stackrel{��}{y}$=bx+a��
��b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$=$\frac{7}{4}$=1.75��
a=$\overline{y}$-b$\overline{x}$=13-1.75��8=-1��
�ع�ֱ�߷���Ϊ$\stackrel{��}{y}$=1.75x-1��
��x=9.6ʱ��$\stackrel{��}{y}$=1.75��9.6-1=15.8��
����Ԥ��רҵ�γɼ�Ϊ9.6�ֵ�ѧ����ҵ�����н15.8��Ԫ��
��3���ٴ���5����ҵ���������ȡ2��������${C}_{5}^{2}$=10��ѡ����
����ǡ��һ����ҵ����רҵ�γɼ�������9����${C}_{3}^{1}$•${C}_{2}^{1}$=6�����Σ�
������ĸ���ΪP=$\frac{6}{10}$=$\frac{3}{5}$��
���� ���⿼�������ϵ�������Իع鷽�̵�Ӧ�����⣬Ҳ�����˹ŵ���͵ĸ��ʼ������⣬���е��⣮


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����0 | B�� | ����0 | C�� | С��0 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{e}{2}$��+�ޣ� | B�� | [0��+�ޣ� | C�� | [-e��+�ޣ� | D�� | [-2e��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��c��a | C�� | c��a��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
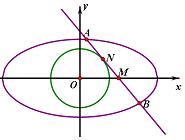 ��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���ҽ���$��\sqrt{3}��0��$���Ҿ�����$��-1��\frac{{\sqrt{3}}}{2}��$����M��x���ϵ�һ�㣬����M��ֱ��l����ԲC����A��B���㣨��A��x����Ϸ���
��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���ҽ���$��\sqrt{3}��0��$���Ҿ�����$��-1��\frac{{\sqrt{3}}}{2}��$����M��x���ϵ�һ�㣬����M��ֱ��l����ԲC����A��B���㣨��A��x����Ϸ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com