
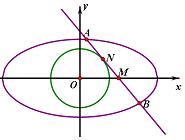
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)分析 (1)由题意列关于a,b的方程组,求解方程组可得a,b的值,则椭圆方程可求;
(2)设出M,A,B的坐标及直线l的方程x=ty+m,与椭圆方程联立,化为关于y的一元二次方程,由|AM|=2|MB|,有y1=-2y2,再结合根与系数的关系可得m与t的关系,由直线与圆相切可得m与t的另一关系式,联立求得m,t的值,可得M的坐标,则|MN|的长可求.
解答 解:(1)由题意知:$\left\{\begin{array}{l}{a^2}-{b^2}={c^2}=3\\ \frac{{{{(-1)}^2}}}{4}+\frac{{{{(-\frac{{\sqrt{3}}}{2})}^2}}}{b^2}=1\end{array}\right.$,
a2=3+b2>3,解得:a2=4,b2=1,
故椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)设M(m,0),直线l:x=ty+m,A(x1,y1),B(x2,y2),
由|AM|=2|MB|,有y1=-2y2,
由$\left\{\begin{array}{l}{x=ty+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(t2+4)y2+2my+m2-4=0,
由韦达定理得:${y_1}+{y_2}=-\frac{2tm}{{{t^2}+4}},{y_1}{y_2}=\frac{{{m^2}-4}}{{{t^2}+4}}$,
由${y_1}{y_2}=-2y_2^2,{y_1}+{y_2}=-2{y_2}+{y_2}=-{y_2}$,
得${y_1}{y_2}=-2{[-({y_1}+{y_2})]^2}=-{({y_1}+{y_2})^2}$,即$\frac{{{m^2}-4}}{{{t^2}+4}},=-2{(-\frac{2tm}{{{t^2}+4}})^2}$,
化简得(m2-4)(t2+4)=-8t2m2,①
原点O到直线的距离$d=\frac{|m|}{{\sqrt{1+{t^2}}}}$,
又直线l与圆$O:{x^2}+{y^2}=\frac{4}{7}$相切,
∴$\frac{|m|}{{\sqrt{1+{t^2}}}}=\sqrt{\frac{4}{7}}$,即${t^2}=\frac{7}{4}{m^2}-1$,②
联立①②得:21m4-16m2-16=0,即(3m2-4)(7m2+4)=0,
解得${m^2}=\frac{4}{3}$,此时${t^2}=\frac{4}{3}$,满足△>0,得$M(±\frac{{2\sqrt{3}}}{3},0)$,
在Rt△OMN中,可得$|{MN}|=\sqrt{\frac{4}{3}-\frac{4}{7}}=\frac{{4\sqrt{21}}}{21}$,
∴|MN|的长为$\frac{{4\sqrt{21}}}{21}$.
点评 本题考查椭圆的简单性质,考查了直线与圆、椭圆位置关系的应用,体现了“设而不求”的解题思想方法,考查计算能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 专业课成绩xi(分) | 7 | 7 | 8 | 9 | 9 |
| 年薪yi(万元) | 10 | 12 | 14 | 14 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{9\sqrt{3}}}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{26}{9}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1,B1C1的中点,求二面角M-EF-N的平面角的余弦值.
如图,正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1,B1C1的中点,求二面角M-EF-N的平面角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com