
分析 (Ⅰ)求出b的值,求出函数的导数,根据f′(1)=ae,求出a的值即可;
(Ⅱ)问题转化为证明$xlnx+5{e^{-2}}>\frac{1}{{2\sqrt{e}}}(x+\frac{1}{2})≥x{e^{-x}}$在(0,1)上恒成立,根据函数的单调性证明即可.
解答 解:( I)$f(1)=\frac{b}{e}=\frac{5}{e}⇒b=5,f'(x)=a{e^x}(lnx+\frac{1}{x})+\frac{{b(x-1){e^{x-2}}}}{x^2}⇒f'(1)=ae=e⇒a=1$;
( II)要证明f(x)>1,即证明xlnx+5e-2>xe-x,
而函数y=xlnx在$(0,\frac{1}{e})$上单减,在$(\frac{1}{e},∞)$上单增,
同时函数$y=\frac{x}{e^x}$在(0,1)上单增,在(1,∞)上单减(此处证明略),
因此只须证明$xlnx+5{e^{-2}}>\frac{1}{{2\sqrt{e}}}(x+\frac{1}{2})≥x{e^{-x}}$在(0,1)上恒成立.
首先证明$g(x)=xlnx+5{e^{-2}}-\frac{1}{{2\sqrt{e}}}(x+\frac{1}{2})>0$,
因$g'(x)=1+lnx-\frac{1}{{2\sqrt{e}}}⇒g'({x_0})=0⇒ln{x_0}$
=$\frac{1}{{2\sqrt{e}}}-1$$(0<{x_0}<1)⇒g({x_0})={x_0}ln{x_0}+5{e^{-2}}-\frac{1}{{2\sqrt{e}}}({x_0}+\frac{1}{2})={x_0}(\frac{1}{{2\sqrt{e}}}-1)+5{e^{-2}}-\frac{1}{{2\sqrt{e}}}({x_0}+\frac{1}{2})$
=$\frac{5}{e^2}+\frac{1}{{4\sqrt{e}}}-{x_0}⇒g(x)≥g({x_0})>0$;
然后证明$h(x)=x{e^{-x}}-\frac{1}{{2\sqrt{e}}}(x+\frac{1}{2})≤0$,
因$h'(x)=\frac{1-x}{e^x}-\frac{1}{{2\sqrt{e}}}⇒h''(x)=\frac{x-2}{e}<0(0<x<1)⇒$h'(x)在(0,1)上单减,
且$h'(\frac{1}{2})=0⇒h(x)$在$(0,\frac{1}{2})$上单增,在$(\frac{1}{2},1)$上单减,$⇒h(x)≤h(\frac{1}{2})=0$.
综上可知,f(x)>1成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{e}{2}$,+∞) | B. | [0,+∞) | C. | [-e,+∞) | D. | [-2e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
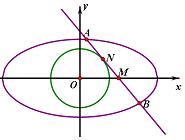 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com