
【题目】在空格内填入“充分非必要”或“必要非充分”或“充要”或“既非充分又非必要”.
(1)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(2)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(3)已知![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(4)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(5)“![]() ”是“AB”的________条件;
”是“AB”的________条件;
(6)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(7)“集合AB”是“![]() ”的________条件;
”的________条件;
(8)已知![]() ,“
,“![]() ”是“
”是“![]() ”的________条件.
”的________条件.
【答案】充分非必要 必要非充分 必要非充分 充分非必要 必要非充分 充分非必要 充分非必要 充要
【解析】
根据充分性、必要性的定义,结合特例法进行判断即可.
(1)若![]() 成立,一定有
成立,一定有![]() 成立;
成立;
当![]() 成立时,
成立时,![]() 不一定成立,例如当
不一定成立,例如当![]() 时,满足
时,满足![]() ,
,
但是![]() ,因此“
,因此“![]() ”是“
”是“![]() ”的充分非必要条件.
”的充分非必要条件.
故答案为:充分非必要
(2)当![]() 成立时,不一定能推出
成立时,不一定能推出![]() ,
,
例如当![]() 时,显然
时,显然![]() 成立,但是
成立,但是![]() ,
,![]() 不成立;
不成立;
当![]() 时,则
时,则![]() 同正或同负,因此有
同正或同负,因此有![]() 成立,
成立,
故“![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
故答案为:必要不充分
(3)当![]() 成立时,不一定能推出
成立时,不一定能推出![]() ,
,
例如当![]() 时,显然
时,显然![]() 成立,但是
成立,但是![]() ,
,
所以已知![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
故答案为:必要不充分
(4)显然由![]() 能推出
能推出![]() ,但由
,但由![]() 不一定能推出
不一定能推出![]() ,
,
例如当![]() 时,显然
时,显然![]() 成立,但是
成立,但是![]() 不成立,
不成立,
所以“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
故答案为:充分不必要
(5)因为由可得![]() ,所以由
,所以由![]() 不一定能推出AB;
不一定能推出AB;
但是由AB,一定能推出![]() ,
,
所以“![]() ”是“AB”的必要不充分条件.
”是“AB”的必要不充分条件.
故答案为:必要不充分
(6)由![]() 根据等式的性质可以推出
根据等式的性质可以推出![]() ,
,
由![]() 不一定能推出
不一定能推出![]() ,例如当
,例如当![]() 时,
时,![]() 成立,但是
成立,但是![]() 不成立.
不成立.
所以“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
故答案为:充分不必要
(7)由AB根据真子集定义可以得到![]() ,
,
由![]() 不一定能推出AB,例如当
不一定能推出AB,例如当![]() 时,显然AB不成立.
时,显然AB不成立.
所以“集合AB”是“![]() ”的充分不必要条件.
”的充分不必要条件.
故答案为:充分不必要
(8)当![]() 时,
时,![]() ,所以由
,所以由![]() 能推出
能推出![]() ,
,
当![]() 时,
时,
若![]() 时,
时,![]() 成立,若
成立,若![]() 时,式子
时,式子![]() 没有意义,
没有意义,
若![]() 时,
时,![]() ,所以有
,所以有![]() .
.
因此由![]() 能推出
能推出![]() .
.
“![]() ”是“
”是“![]() ”的充要条件.
”的充要条件.
故答案为:充要


科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的左焦点,离心率为
的左焦点,离心率为![]() ,直线
,直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中点,
的中点,![]() 是椭圆
是椭圆![]() 上一点,求
上一点,求![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人同时从A地赶往B地,甲先骑自行车到中点改为跑步,而乙则是先跑步,到中点后改为骑自行车,最后两人同时到达B地.已知甲骑自行车比乙骑自行车快.若每人离开甲地的距离![]() 与所用时间
与所用时间![]() 的函数用图象表示,则甲、乙对应的图象分别是
的函数用图象表示,则甲、乙对应的图象分别是
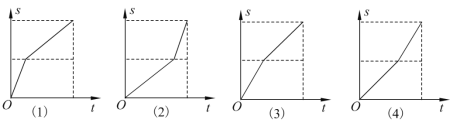
A.甲是(1),乙是(2)B.甲是(1),乙是(4)
C.甲是(3),乙是(2)D.甲是(3),乙是(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2+ax-a),其中a是常数.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若存在实数k,使得关于x的方程f(x)=k在[0,+∞)上有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com