
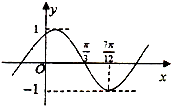
 已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )| A. | 向右平移 $\frac{π}{6}$个长度单位 | B. | 向右平移 $\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移 $\frac{π}{12}$个长度单位 |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式,再利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:由函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象可得A=1,
$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,求得ω=2.
再根据五点法作图可得2×$\frac{π}{3}$+φ=π,∴φ=$\frac{π}{3}$,f(x)=sin(2x+$\frac{π}{3}$).
故把f(x)=sin(2x+$\frac{π}{3}$)的图象向右平移 $\frac{π}{6}$个长度单位,可得y=sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=g(x)的图象,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | ln(x2+1)>ln(y2+1) | B. | sinx>siny | C. | x3>y3 | D. | $\frac{1}{{{x^2}+1}}>\frac{1}{{{y^2}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | y | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{36}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com