
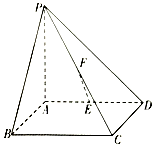
 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.分析 (1)取PB的中点为G,连接AG,FG,推导出EF∥AG,由此能证明EF∥平面PAB.
(2)由VP-AEF=VF-PAE,能求出三棱锥P-AEF的体积.
解答 证明:(1)取PB的中点为G,连接AG,FG,
∵E,F分别为AD,PC的中点,四棱锥P-ABCD的底面是正方形,
∴GF$\underset{∥}{=}$AE,∴AEFG是平行四边形,∴EF∥AG,
∵EF?平面PAB,AG?平面PAB,
∴EF∥平面PAB.
解:(2)∵PA=AB=2,PA⊥底面ABCD,
∴三棱锥P-AEF的体积${V_{P-AEF}}={V_{F-PAE}}=\frac{1}{3}×\frac{1}{2}×2×1×1=\frac{1}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{49π}{12}$ | B. | $\frac{35π}{6}$ | C. | $\frac{25π}{6}$ | D. | $\frac{17π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
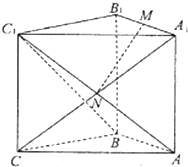 直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.
直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com