
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 p1:求出函数的导数,通过讨论a的范围结合函数的单调性求出a的范围即可;
p2:根据奇函数的定义判定即可;
p3:对表达式变形可得f(x)=x+$\frac{1}{x+1}$=x+1+$\frac{1}{x+1}$-1,利用均值定理判定即可;
p4:先求导函数,函数f(x)=x(lnx-ax)有两个极值点,等价于f′(x)=lnx-2ax+1有两个零点,等价于函数y=lnx与y=2ax-1的图象由两个交点,在同一个坐标系中作出它们的图象.由图可求得实数a的取值范围.
解答 解:关于命题p1,f′(x)=$\left\{\begin{array}{l}{2ax,x≥0}\\{a(a+2{)e}^{ax},x<0}\end{array}\right.$;
∴(1)若a>0,x≥0时,f′(x)≥0,
即函数f(x)在[0,+∞)上单调递增,且ax2+1≥1;
要使f(x)在R上为单调函数则x<0时,a(a+2)>0,
∵a>0,∴解得a>0,并且(a+2)eax<a+2,
∴a+2≤1,解得a≤-1,不符合a>0,
∴这种情况不存在;
(2)若a<0,x≥0时,f′(x)≤0,
即函数f(x)在[0,+∞)上单调递减,且ax2+1≤1;
要使f(x)在R上为单调函数,则x<0时,a(a+2)<0,
解得-2<a<0,并且(a+2)eax>a+2,
∴a+2≥1,解得a≥-1,∴-1≤a<0;
综上得a的取值范围为[-1,0);
故命题p1是假命题;
关于命题p2:根据奇函数的定义可知,
f(-x)=2-x-2x=-f(x),故?x∈R,f(-x)=-f(x),
故命题p2正确;
p3:若f(x)=x+$\frac{1}{x+1}$=x+1+$\frac{1}{x+1}$-1≥1,
且当x=0时,等号成立,故不存在x0∈(0,+∞),f(x0)=1,
故命题p3错误;
由题意,y′=lnx+1-2ax
令f′(x)=lnx-2ax+1=0得lnx=2ax-1,
函数y=xlnx-ax2有两个极值点,等价于f′(x)=lnx-2ax+1有两个零点,
等价于函数y=lnx与y=2ax-1的图象有两个交点,
在同一个坐标系中作出它们的图象(如图)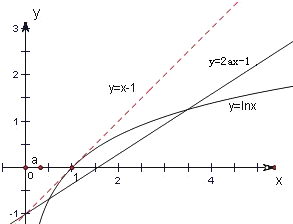
当a=$\frac{1}{2}$时,直线y=2ax-1与y=lnx的图象相切,
由图可知,当0<a<$\frac{1}{2}$时,y=lnx与y=2ax-1的图象有两个交点.
则实数a的取值范围是(0,$\frac{1}{2}$);
故命题p4正确,
故选:B.
点评 本题考查均值不等式,主要考查函数的零点以及数形结合方法,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
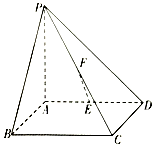 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>c>a | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | (0,e) | C. | (-∞,$\frac{1}{e}$) | D. | (0,$\frac{1}{e}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com