
分析 利用正弦定理求出C,求出三角形的外接圆的半径,然后利用两角和的正弦函数公式以及正弦定理求出a+b+c的取值范围.
解答 解:由acosB+bcosA=$\frac{\sqrt{3}c}{2sinC}$,得sinAcosB+sinBcosA=$\frac{\sqrt{3}sinC}{2sinC}$,
即sin(A+B)=sinC=$\frac{\sqrt{3}}{2}$,
因为角C是锐角,
所以C=$\frac{π}{3}$,
所以A+B=$\frac{2π}{3}$,2R=$\frac{c}{sinC}$=$\frac{2}{sin\frac{π}{3}}$=$\frac{4\sqrt{3}}{3}$,
所以三角形周长l=a+b+c=2R(sinA+sinB+sinC)=$\frac{4\sqrt{3}}{3}$(sinA+sin($\frac{2π}{3}$-A)+sin$\frac{π}{3}$)=4sin(A+$\frac{π}{6}$)+2,
又因为 0<A<$\frac{π}{2}$,
所以:A+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{2π}{3}$),
所以:sin(A+$\frac{π}{6}$)∈($\frac{1}{2}$,1],
所以:周长l=a+b+c=4sin(A+$\frac{π}{6}$)+2∈(4,6].
故答案为:(4,6].
点评 本题考查正弦定理以及余弦定理的应用,考查三角形的解法,考查了转化思想,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | $[3+2\sqrt{2}\;\;,\;\;+∞)$ | C. | [6,+∞) | D. | $(4\;\;,\;\;3+2\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
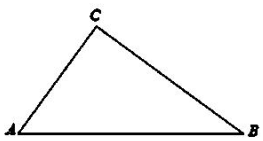 如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{3}}{2}$,1) | B. | [$\frac{\sqrt{6}}{3}$,1) | C. | (0,$\frac{\sqrt{3}}{2}$] | D. | (0,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com