
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销,定价为1000元/件.
(1)设日销售40个零件的概率为![]() ,记5天中恰有2天销售40个零件的概率为
,记5天中恰有2天销售40个零件的概率为![]() ,写出
,写出![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 极大值点
极大值点![]() .
.
(2)试销结束后统计得到该4S店这30内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 |
其中,有两个数据未给出.试销结束后,这款零件正式上市,每件的定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有55件,批发价为550元/件;小箱每箱有40件,批发价为600元/件,以这30天统计的各日销售量的频率作为试销后各日销售量发生的概率.该4S店决定每天批发两箱,若同时批发大箱和小箱,则先销售小箱内的零件,同时根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店,假设日销售量为80件的概率为![]() ,其中
,其中![]() 为(1)中
为(1)中![]() 的极大值点.
的极大值点.
(i)设该4S店批发两大箱,当天这款零件的利润为随机变量![]() ;批发两小箱,当天这款零件的利润为随机变量
;批发两小箱,当天这款零件的利润为随机变量![]() ,求
,求![]() 和
和![]() ;
;
(ii)以日利润的数学期望作为决策依据,该4S店每天应该按什么方案批发零件?
【答案】(1)![]() ,
,![]() .(2)(i)
.(2)(i)![]() =2.526万元,
=2.526万元,![]() =2.28万元;(ii)两大箱
=2.28万元;(ii)两大箱
【解析】
(1)利用二项式定理求出![]() 关于
关于![]() 函数,对函数
函数,对函数![]() 进行求导,利用导数判断函数
进行求导,利用导数判断函数![]() 的单调性求出极大值点
的单调性求出极大值点![]() 即可;
即可;
(2)(i)利用(1)中![]() 的值,分别求出日销售量为40件,60件,80件,100件的概率,然后求出批发为两大箱时所对应的利润,代入数学期望公式求出
的值,分别求出日销售量为40件,60件,80件,100件的概率,然后求出批发为两大箱时所对应的利润,代入数学期望公式求出![]() ;求出批发为两小箱时所对应的利润,代入数学期望公式求出
;求出批发为两小箱时所对应的利润,代入数学期望公式求出![]() 即可;
即可;
(ii)设当该4S店批发一大箱和一小箱时,成本为54250元,当天这款零件的利润为随机变量![]() ,分别求出日销售量分别为40件,60件,80件,100件的利润,代入数学期望公式求出
,分别求出日销售量分别为40件,60件,80件,100件的利润,代入数学期望公式求出![]() ,比较
,比较![]() 、
、![]() 和
和![]() 的大小即可.
的大小即可.
(1)由题意可得,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 有极大值,故
有极大值,故![]() .
.
(2)由题意可知,日销售量为80件的概率为![]() ,
,
日销售量为60件的概率为![]() ,日销售量为40件的概率为
,日销售量为40件的概率为![]() ,
,
所以日销售量为100的概率为![]() .
.
(i)批发两大箱,则批发成本为60500元,
当日销售量为40件时,利润为![]() (万元);
(万元);
当日销售量为60件时,利润为![]() (万元);
(万元);
当日销售量为80件时,利润为![]() (万元);
(万元);
当日销售量为100件时,利润为![]() (万元),
(万元),
所以![]() (万元).
(万元).
若批发两小箱,则批发成本为48000元,
当日销售量为40件时,利润为![]() (万元);
(万元);
当日销售量为60件时,利润为![]() (万元);
(万元);
当日销售量为80件或100件时,利润为![]() (万元),
(万元),
所以![]() (万元);
(万元);
(ii)当该4S店批发一大箱和一小箱时,成本为54250元,当天这款零件的利润为随机变量![]() ,
,
当日销售量为40件时,利润为![]() (万元);
(万元);
当日销售量为60件时,利润为![]() (万元);
(万元);
当日销售量为80件时,利润为![]() (万元);
(万元);
当日销售量为100件时,利润为![]() (万元);
(万元);
所以![]() (万元),
(万元),
所以![]() ,故该4S店每天应该批发两大箱.
,故该4S店每天应该批发两大箱.


科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,若在线段
为虚轴的一个端点,若在线段![]() (不含端点)上存在两点
(不含端点)上存在两点![]() ,
,![]() ,使得
,使得![]() ,则双曲线的渐近线斜率的平方的取值范围是( )
,则双曲线的渐近线斜率的平方的取值范围是( )
A.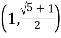 B.
B.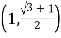
C.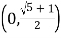 D.
D.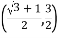
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对应的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,求cosB的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b∈R.则“关于x的方程![]() 有两个不等实数根”是“a >|b|+1”的( )
有两个不等实数根”是“a >|b|+1”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“芝麻开门”娱乐活动中,共有![]() 扇门,游戏者根据规则开门,并根据打开门的数量获取相应奖励.已知开每扇门相互独立,且规则相同,开每扇门的规则是:从给定的
扇门,游戏者根据规则开门,并根据打开门的数量获取相应奖励.已知开每扇门相互独立,且规则相同,开每扇门的规则是:从给定的![]() 把钥匙(其中有且只有
把钥匙(其中有且只有![]() 把钥匙能打开门)中,随机地逐把抽取钥匙进行试开,钥匙使用后不放回.若门被打开,则转为开下一扇门;若连续
把钥匙能打开门)中,随机地逐把抽取钥匙进行试开,钥匙使用后不放回.若门被打开,则转为开下一扇门;若连续![]() 次未能打开,则放弃这扇门,转为开下一扇门;直至
次未能打开,则放弃这扇门,转为开下一扇门;直至![]() 扇门都进行了试开,活动结束.
扇门都进行了试开,活动结束.
(1)设随机变量![]() 为试开第一扇门所用的钥匙数,求
为试开第一扇门所用的钥匙数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)求恰好成功打开![]() 扇门的概率.
扇门的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: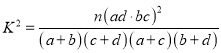 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点,其中直线l不过原点.
两点,其中直线l不过原点.
(1)求椭圆C的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,其中
,其中![]() 且
且![]() .记
.记![]() 的面积为S.分别以
的面积为S.分别以![]() 为直径的圆的面积依次为
为直径的圆的面积依次为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com