
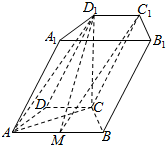
 ��ͼ��ʾ����������ABCD-A1B1C1D1�У�����ABCDΪ�������Σ���DAB=60�㣬AB=2CD=2����CD1��ֱ��ƽ��ABCD����$C{D_1}=\sqrt{3}$��M���߶�AB���е㣮
��ͼ��ʾ����������ABCD-A1B1C1D1�У�����ABCDΪ�������Σ���DAB=60�㣬AB=2CD=2����CD1��ֱ��ƽ��ABCD����$C{D_1}=\sqrt{3}$��M���߶�AB���е㣮���� ��1������AC���Ƶ���AC��BC��BC��CD1���Ӷ�BC����ACD1���ɴ���֤��BC��AD1��
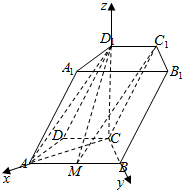
��2����CΪԭ�㣬CAΪx�ᣬCBΪy�ᣬCD1Ϊz�ᣬ�����ռ�ֱ������ϵ�������������������$\frac{CN}{AC}$=$\frac{1}{2}$ʱ��ʹ��D1N��ƽ��C1D1M���ɽǵ�����ֵΪ$\frac{1}{5}$��
���  ֤������1������AC���ڡ�ABC�У�AB=2��AC=$\sqrt{3}$��BC=1��
֤������1������AC���ڡ�ABC�У�AB=2��AC=$\sqrt{3}$��BC=1��
��BC2+AC2=AB2����AC��BC��
�֡�CD1����ABCD��BC?��ABCD����BC��CD1��
��AC��CD1=C��AC?��ACD1��CD1?��ACD1��
��BC����ACD1��
��AD1?��ACD1����BC��AD1��
�⣺��2����$\frac{CN}{AC}$=$\frac{1}{2}$ʱ��ʹ��D1N��ƽ��C1D1M���ɽǵ�����ֵΪ$\frac{1}{5}$��
֤�����£�
��CΪԭ�㣬CAΪx�ᣬCBΪy�ᣬCD1Ϊz�ᣬ�����ռ�ֱ������ϵ��
C��0��0��0����A��$\sqrt{3}��0��0$����B��0��1��0����M��$\frac{\sqrt{3}}{2}��-\frac{1}{2}��0$����D1��0��0��$\sqrt{3}$����
��$\overrightarrow{C{C}_{1}}$=$\overrightarrow{D{D}_{1}}$����C1��-$\frac{\sqrt{3}}{2}$��$\frac{1}{2}$��$\sqrt{3}$����
��N��a��0��0������0��a��$\sqrt{3}$����
����ķ�����$\overrightarrow{m}$=��x��y��z����
��$\left\{\begin{array}{l}{\overrightarrow{{C}_{1}{D}_{1}}•\overrightarrow{m}=0}\\{\overrightarrow{{C}_{1}M}=0}\end{array}\right.$����$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{z=x}\end{array}\right.$��ȡx=1����$\overrightarrow{m}$=��1��$\sqrt{3}$��1����
$\overrightarrow{{D}_{1}N}$=��a��0��-$\sqrt{3}$����
������|cos��$\overrightarrow{{D}_{1}N}$��$\overrightarrow{m}$��|=$\frac{|a-\sqrt{3}|}{\sqrt{{a}^{2}+3}•\sqrt{5}}$=$\frac{1}{5}$��]
���a=$\frac{\sqrt{3}}{2}$��a=2$\sqrt{3}$���ᣩ��
�൱$\frac{CN}{AC}$=$\frac{1}{2}$ʱ��ʹ��D1N��ƽ��C1D1M���ɽǵ�����ֵΪ$\frac{1}{5}$��
���� ���⿼������ֱ�ߴ�ֱ��֤�����������������ĵ��Ƿ���ڵ��ж��������е��⣬����ʱҪ�������⣬ע���������ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=2 | B�� | m��2 | C�� | m��2 | D�� | m��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-3���ȣ�-3��0] | B�� | ��-�ޣ�-3���ȣ�-3��1] | C�� | ��-3��0] | D�� | ��-3��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R��x2+5x��6 | B�� | ?x��R��x2+5x=6 | C�� | ?x0��R��x02+5x0��6 | D�� | ?x��R��x02+5x0��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��a2 | B�� | 2��a2 | C�� | $\frac{3��{a}^{2}}{2}$ | D�� | $\frac{��{a}^{2}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com