
分析 连结DE,推导出$\frac{MD}{MA}=\frac{1}{6}$,同理,$\frac{NE}{NB}=\frac{1}{6}$,由此能求出$\frac{{S}_{△LMN}}{{S}_{△ABC}}$的值.
解答 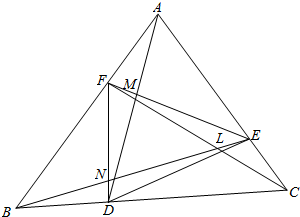 解:连结DE,有S△BCE=$\frac{2}{9}$S△ABC,${S}_{△BDE}=\frac{1}{9}{S}_{△ABC}$,
解:连结DE,有S△BCE=$\frac{2}{9}$S△ABC,${S}_{△BDE}=\frac{1}{9}{S}_{△ABC}$,
∴${S}_{△ABE}=\frac{6}{9}{S}_{△ABC}$,∴$\frac{MD}{MA}=\frac{1}{6}$,
同理,$\frac{NE}{NB}=\frac{1}{6}$,
设S△BMD=1,则S△ABC=21,S△BMA=6,S△ABD=7,S△BEC=7,
∴S△AME=21-7-7+1=8,
∴$\frac{BM}{ME}=\frac{3}{4}$,∴MN=MB,LM=3MD,
∴$\frac{{S}_{△LMN}}{{S}_{△ABC}}$=$\frac{1}{7}$.
故答案为:$\frac{1}{7}$.
点评 本题考查两个三角形面积比的求法,是中档题,解题时要认真审题,注意三角形面积公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
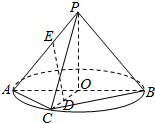 如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.
如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
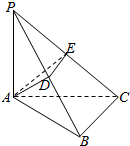 如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=$\frac{π}{2}$,E、F依次为CC1和BC的中点:
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=$\frac{π}{2}$,E、F依次为CC1和BC的中点:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
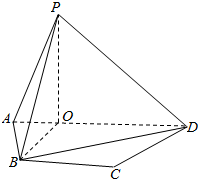 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
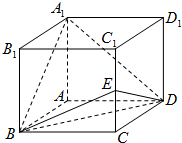 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
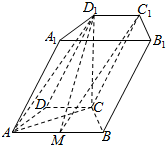 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com