
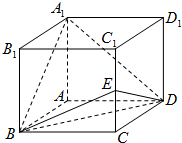
 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.分析 (1)(方法一)设AB=a,AA1=b,连接AC交BD于O,说明∠A1OE是二面角A1-BD-E的平面角,利用勾股定理${A_1}{E^2}={A_1}{O^2}+E{O^2}=\frac{9}{4}{b^2}$,$∠{A_1}OE=\frac{π}{2}$,证明平面A1BD⊥平面BDE.
(方法二)连接AC交BD于O,则AC⊥BD,作OG∥CC1,以O为原点,$\overrightarrow{OC}$、$\overrightarrow{OD}$、$\overrightarrow{OG}$所在方向为x轴、y轴、z轴正方向建立空间直角坐标系,设AB=a,AA1=b,通过数量积$\overrightarrow{OE}•\overrightarrow{{A_1}B}=\frac{1}{4}{a^2}-\frac{1}{2}{b^2}=0$,证明OE⊥A1B,OE⊥A1D,推出OE⊥平面A1BD,即可证明平面A1BD⊥平面BDE.
(2)(方法一)连接B1C交BE于F,说明∠CFE是直线A1D与直线BE所成的角,利用△BB1F~△ECF,通过余弦定理求解即可.
(方法二)作OG∥CC1,以O为原点,$\overrightarrow{OC}$、$\overrightarrow{OD}$、$\overrightarrow{OG}$所在方向为x轴、y轴、z轴正方向建立空间直角坐标系,利用向量的数量积求解所求角的余弦值即可.
解答 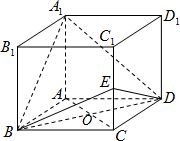 证明:(1)(方法一)设AB=a,AA1=b,则${A_1}B={A_1}D=\sqrt{{a^2}+{b^2}}$,$EB=ED=\sqrt{{a^2}+{{(\frac{1}{2}b)}^2}}$…(2分)
证明:(1)(方法一)设AB=a,AA1=b,则${A_1}B={A_1}D=\sqrt{{a^2}+{b^2}}$,$EB=ED=\sqrt{{a^2}+{{(\frac{1}{2}b)}^2}}$…(2分)
连接AC交BD于O,则BO=DO,$AO=CO=\frac{1}{2}a$,$BD=\sqrt{3}a$…(3分)
所以A1O⊥BD,EO⊥BD,∠A1OE是二面角A1-BD-E的平面角…(4分)
${A_1}O=\sqrt{A{A_1}^2+A{O^2}}=\sqrt{{{(\frac{1}{2}a)}^2}+{b^2}}$,$EO=\sqrt{C{E^2}+C{O^2}}=\sqrt{{{(\frac{1}{2}a)}^2}+{{(\frac{1}{2}b)}^2}}$,${A_1}E=\sqrt{{A_1}{C_1}^2+{C_1}{E^2}}=\sqrt{{a^2}+{{(\frac{1}{2}b)}^2}}$…(5分)
因为A1B⊥A1D,所以3a2=2(a2+b2),即a2=2b2…(6分)
${A_1}{E^2}={A_1}{O^2}+E{O^2}=\frac{9}{4}{b^2}$,$∠{A_1}OE=\frac{π}{2}$,平面A1BD⊥平面BDE…(7分)
(方法二)连接AC交BD于O,则AC⊥BD,作OG∥CC1,以O为原点,$\overrightarrow{OC}$、$\overrightarrow{OD}$、$\overrightarrow{OG}$所在方向为x轴、y轴、z轴正方向建立空间直角坐标系…(1分)
设AB=a,AA1=b,则$AO=CO=\frac{1}{2}a$,$CE=\frac{1}{2}b$,$BO=DO=\frac{{\sqrt{3}}}{2}a$…(2分)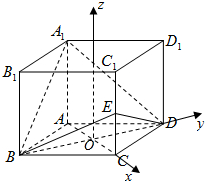
${A_1}(-\frac{1}{2}a,0,b)$,$B(0,-\frac{{\sqrt{3}}}{2}a,0)$,$D(0,\frac{{\sqrt{3}}}{2}a,0)$,$E(\frac{1}{2}a,0,\frac{1}{2}b)$…(3分)
$\overrightarrow{OE}=(\frac{1}{2}a,0,\frac{1}{2}b)$,$\overrightarrow{{A_1}B}=(\frac{1}{2}a,-\frac{{\sqrt{3}}}{2}a,-b)$,$\overrightarrow{{A_1}D}=(\frac{1}{2}a,\frac{{\sqrt{3}}}{2}a,-b)$…(4分),
依题意,$\overrightarrow{{A_1}B}•\overrightarrow{{A_1}D}=\frac{1}{4}{a^2}-\frac{3}{4}{a^2}+{b^2}=0$,a2=2b2…(5分)
所以$\overrightarrow{OE}•\overrightarrow{{A_1}B}=\frac{1}{4}{a^2}-\frac{1}{2}{b^2}=0$,$\overrightarrow{OE}•\overrightarrow{{A_1}D}=\frac{1}{4}{a^2}-\frac{1}{2}{b^2}=0$…(6分)
OE⊥A1B,OE⊥A1D,A1B∩A1D=A1,所以OE⊥平面A1BD,又OE?平面BDE,
所以平面A1BD⊥平面BDE…(7分)
(2)解:(方法一)连接B1C交BE于F,则B1C∥A1D,∠CFE是直线A1D与直线BE所成的角…(8分)
由BB1∥CC1,△BB1F~△ECF得,$EF=\frac{1}{3}EB=\frac{1}{2}b$,$CF=\frac{1}{3}{B_1}C=\frac{{\sqrt{3}}}{3}b$…(10分)$cos∠CFE=\frac{{E{F^2}+C{F^2}-C{E^2}}}{2EF×CF}=\frac{{\sqrt{3}}}{3}$…(12分)
(方法二)作OG∥CC1,以O为原点,$\overrightarrow{OC}$、$\overrightarrow{OD}$、$\overrightarrow{OG}$所在方向为x轴、y轴、z轴正方向建立空间直角坐标系…(8分)
则$B(0,-\frac{{\sqrt{3}}}{2}a,0)$,$E(\frac{1}{2}a,0,\frac{1}{2}b)$,$D(0,\frac{{\sqrt{3}}}{2}a,0)$,${A_1}(-\frac{1}{2}a,0,b)$…(9分)
(无论第(1)问是否建立空间直角坐标系,正确写出各点坐标这一步都给到9分)
$\overrightarrow{BE}=(\frac{1}{2}a,\frac{{\sqrt{3}}}{2}a,\frac{1}{2}b)$,$\overrightarrow{{A_1}D}=(\frac{1}{2}a,\frac{{\sqrt{3}}}{2}a,-b)$…(10分)
所求角的余弦值为$cosθ=\frac{{\overrightarrow{BE}•\overrightarrow{{A_1}D}}}{{|\overrightarrow{BE}|×|\overrightarrow{{A_1}D}|}}=\frac{{\sqrt{3}}}{3}$…(12分)
点评 本题考查与二面角有关的立体几何问题,平面与平面垂直的判断,异面直线市场价的求法,考查空间想象能力以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
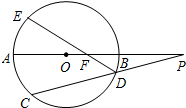 如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.
如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(-3,0] | B. | (-∞,-3)∪(-3,1] | C. | (-3,0] | D. | (-3,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com