
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 分$\overrightarrow{a}$,$\overrightarrow{b}$共线和不共线判断①,利用已知条件判断以$\overrightarrow{a}$,$\overrightarrow{b}$为邻边的四边形的形状可得②③④的真假,则答案可求.
解答 解:由$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$为非零向量,且$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$,$\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{d}$,得
①若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,当$\overrightarrow{a}$、$\overrightarrow{b}$共线时,$\overrightarrow{c}$或$\overrightarrow{d}$为$\overrightarrow{0}$,满足$\overrightarrow{c}$•$\overrightarrow{d}$=0,
当$\overrightarrow{a}$、$\overrightarrow{b}$不共线时,可知以$\overrightarrow{a}$,$\overrightarrow{b}$为邻边的四边形的形状是菱形,则$\overrightarrow{c}$•$\overrightarrow{d}$=0,①正确;
②若$\overrightarrow{c}$•$\overrightarrow{d}$=0,可得:($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,即${\overrightarrow{a}}^{2}={\overrightarrow{b}}^{2}$,则|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,②正确;
③若|$\overrightarrow{c}$|=|$\overrightarrow{d}$|,可知以$\overrightarrow{a}$,$\overrightarrow{b}$为邻边的四边形的形状是矩形,则$\overrightarrow{a}•\overrightarrow{b}=0$,③正确;
④若$\overrightarrow{a}$•$\overrightarrow{b}$=0,可知以$\overrightarrow{a}$,$\overrightarrow{b}$为邻边的四边形的形状是矩形,则|$\overrightarrow{c}$|=|$\overrightarrow{d}$|,④正确.
故选:D.
点评 本题考查命题的真假的判断与应用,向量的数量积运算及其几何意义,是中档题.


科目:高中数学 来源: 题型:解答题
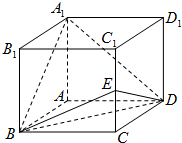 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
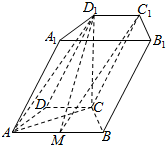 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
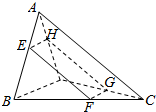 空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.
空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | ($\frac{9}{2}$,$\frac{11}{2}$) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | a+b+c | D. | ab+bc+ca |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com