
分析 由题意和三角函数公式可得sinBsinC=$\frac{3}{4}$,再由a2=bc和正弦定理可得sinA,解得A验证可得.
解答 解:∵△ABC中cos(B-C)+cosA=$\frac{3}{2}$,
∴cos(B-C)-cos(B+C)=$\frac{3}{2}$,
∴cosBcosC+sinBsnC-(cosBcosC-sinBsnC)=$\frac{3}{2}$,
∴2sinBsnC=$\frac{3}{2}$,sinBsinC=$\frac{3}{4}$,
再由a2=bc和正弦定理可得sin2A=sinBsinC=$\frac{3}{4}$,
由三角形中sinA>0可得sinA=$\frac{\sqrt{3}}{2}$,∴A=$\frac{π}{3}$或$\frac{2π}{3}$,
若A=$\frac{2π}{3}$,则cos(B-C)+cosA=cos(B-C)-$\frac{1}{2}$=$\frac{3}{2}$,
∴cos(B-C)=2,显然矛盾,应舍去
故答案为:$\frac{π}{3}$.
点评 本题考查正余弦定理解三角形,注意去掉一解是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
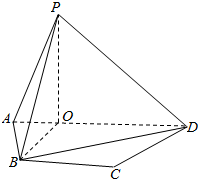 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
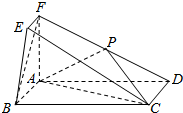 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
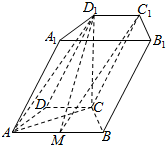 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
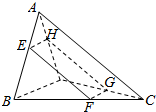 空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.
空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | ($\frac{9}{2}$,$\frac{11}{2}$) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-5=0 | B. | x-2y+3=0 | C. | 2x+y-4=0 | D. | 2x-y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com