
分析 (1)在△ABM中,利用余弦定理计算BM;
(2)以BC的中点为原点建立坐标系,设M(t,0),N(t+1,0),用t表示出$\overrightarrow{AM}•\overrightarrow{AN}$的函数,利用t的范围和二次函数的性质得出答案.
解答 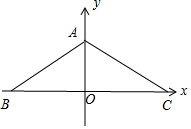 解:(1)在△ABM中,由余弦定理得:
解:(1)在△ABM中,由余弦定理得:
AM2=BM2+AB2-$\sqrt{3}$AB•BM,
即7=BM2+12-$\sqrt{3}•2\sqrt{3}•BM$,解得:BM=1或BM=5.
(2)取BC得中点O,连接AO,
以BC,OA为x轴,y轴建立平面直角坐标系,
则A(0,$\sqrt{3}$),B(-3,0),C(3,0),
设M(t,0),N(t+1,0),则$\overrightarrow{AM}$=(t,-$\sqrt{3}$),$\overrightarrow{AN}$=(t+1,-$\sqrt{3}$),
∴$\overrightarrow{AM}•\overrightarrow{AN}$=t2+t+3=(t+$\frac{1}{2}$)2+$\frac{11}{4}$(-3≤t≤2),
∴当t=-$\frac{1}{2}$时,$\overrightarrow{AM}•\overrightarrow{AN}$取得最小值$\frac{11}{4}$,当t=2时,$\overrightarrow{AM}•\overrightarrow{AN}$取得最大值9.
∴$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[$\frac{11}{4}$,9].
点评 本题考查了平面向量的数量积运算,解三角形,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 若$f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
若$f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com