练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知函数f（x）=x2-6x+8，x∈[1，a]，并且f（x）的最大值为f（a），那么实数a的取值范围是[5，+∞）．

    分析 由题意可知函数的对称轴x=3，结合二次函数的对称性可知，要使得函数f（x）在（1，a]函数f（x）的最大值为f（a）可求a的范围

    解答 解：∵f（x）=x2-6x+8的对称轴x=3
    ∵f（x）=x2-6x+8，x∈[1，a]，并且函数f（x）的最大值为f（a）
    ∵f（1）=f（5）
    ∴a≥5
    故答案为[5，+∞）

    点评 本题主要考查了二次函数的在闭区间上的最值求解，解题的关键是二次函数的对称性的应用

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

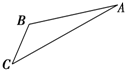    5．如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50m/min．在甲出发2min 后，乙从A乘缆车到B，在B处停留1min后，再从B匀速步行到C．假设缆车匀速直线运行的速度为130m/min，山路AC长为1260m，经测量，cos A=$\frac{12}{13}$，cos C=$\frac{3}{5}$．
    （Ⅰ）求索道AB的长；
    （Ⅱ）问：乙出发多少分钟后，乙在缆车上与甲的距离最短？
    （Ⅲ）为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．一个几何体的三视图如图所示，那么这个几何体的体积是（　　）
    A．4B．6C．8D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．与曲线$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{49}$=1共焦点，且与曲线$\frac{{y}^{2}}{36}$-$\frac{{x}^{2}}{64}$=1共渐近线的双曲线方程为（　　）
    A．$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1B．$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1C．$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1D．$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列函数中，最小值是4的函数是（　　）
    A．y=x+$\frac{4}{x}$B．y=sinx+$\frac{4}{sinx}$（0＜x＜π）
    C．y=ex+4e-xD．$y={log_3}x+\frac{4}{{{{log}_3}x}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设函数f（x）=Acos（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）．若f（x）在区间[0，$\frac{2π}{3}$]上具有单调性，且f（-$\frac{π}{3}$）=f（0）=-f（$\frac{2π}{3}$），则ω=$\frac{6}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．三棱锥A-BCD中，已知AB=CD=$\sqrt{5}$，AD=BC=$\sqrt{6}$，AC=BD=$\sqrt{7}$，那么该三棱锥外接球的表面积为（　　）
    A．6πB．7πC．9πD．12π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．三个数log2$\frac{1}{5}$，20.1，2-1的大小关系是（　　）
    A．${log_2}\frac{1}{5}\;＜{2^{0.1}}\;＜{2^{-1}}$B．${log_2}\frac{1}{5}\;＜{2^{-1}}＜{2^{0.1}}$
    C．${2^{0.1}}\;＜{2^{-1}}＜{log_2}\frac{1}{5}$D．${2^{0.1}}\;＜{log_2}\frac{1}{5}＜{2^{-1}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．sin$\frac{π}{12}$cos$\frac{π}{12}$=$\frac{1}{4}$．

    查看答案和解析>>

    同步练习册答案