
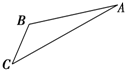
 如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min 后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130m/min,山路AC长为1260m,经测量,cos A=$\frac{12}{13}$,cos C=$\frac{3}{5}$.
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min 后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130m/min,山路AC长为1260m,经测量,cos A=$\frac{12}{13}$,cos C=$\frac{3}{5}$.分析 (Ⅰ)由题意可知sin B=sin(A+C)=sin Acos C+cos Asin C,求得sinB,由正弦定理可知:$\frac{AB}{sinC}$=$\frac{AC}{sinB}$,即可求得AB的长;
(Ⅱ)设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,由余弦定理可得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×$\frac{12}{13}$=200(37t2-70t+50).根据二次函数的性质当t=$\frac{35}{37}$min时,甲、乙两游客距离最短;
(Ⅲ)由正弦定理求得BC=500m,甲已走了50×(2+8+1)=550 m,还需走710 m才能到达C,由题意可知:-3≤$\frac{500}{v}$-$\frac{710}{50}$≤3,即可求得乙步行的速度应控制在什么范围.
解答 解:(Ⅰ)在△ABC中,cos A=$\frac{12}{13}$,cos C=$\frac{3}{5}$,
∴sin A=$\frac{5}{13}$,sinC=$\frac{4}{5}$,
∴sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+cos Asin C=$\frac{5}{13}$×$\frac{3}{5}$+$\frac{12}{13}$×$\frac{4}{5}$=$\frac{63}{65}$,
由正弦定理$\frac{AB}{sinC}$=$\frac{AC}{sinB}$,可得:AB=$\frac{AC}{sinB}$•sinC=$\frac{1260}{\frac{63}{65}}$×$\frac{4}{5}$=1040m,
∴索道AB的长为1040 m.
(Ⅱ)假设乙出发t min后,甲、乙两游客距离为d,此时,甲行走了(100+50t) m,乙距离A处130t m,
∴由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×$\frac{12}{13}$=200(37t2-70t+50).
∵0≤t≤$\frac{1040}{130}$,即0≤t≤8,
故当t=$\frac{35}{37}$min时,甲、乙两游客距离最短.
(Ⅲ)由正弦定理$\frac{BC}{sinA}$=$\frac{AC}{sinB}$,得BC=$\frac{AC}{sinB}$•sin A=$\frac{1260}{\frac{63}{65}}$×$\frac{3}{15}$=500 m.
乙从B出发时,甲已走了50×(2+8+1)=550 m,还需走710 m才能到达C,
设乙步行的速度为v m/min,由题意得-3≤$\frac{500}{v}$-$\frac{710}{50}$≤3,
解得:$\frac{1250}{43}$≤v≤$\frac{625}{14}$,
∴为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在[$\frac{1250}{43}$,$\frac{625}{14}$](单位:m/min)范围内.
点评 本题考查正弦定理及余弦定理的应用,考查了同角三角函数的基本关系、及不等式解法和解三角形的实际应用等知识,考查分类讨论及数形结合的思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com