
. |
| z |
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.
如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
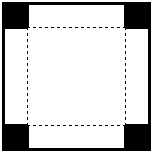 如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com