
分析 (1)设圆P的方程为x2+y2+Dx+Ey+F=0,利用待宝系数法能求出圆P的方程.
(2)圆P的圆心P(-3,0),半径r=5,圆Q的圆心Q(0,a),半径r=2,由圆P和圆Q相外切,得|PQ|=5+2=7,由此利用两点间距离公式能求出a.
解答 解:(1)设圆P的方程为x2+y2+Dx+Ey+F=0,
∵圆P过A(-8,0),B(2,0),C(0,4)三点,
∴$\left\{\begin{array}{l}{64-8D+F=0}\\{4+2D+F=0}\\{16+4E+F=0}\end{array}\right.$,解得D=6,E=0,F=-16,
∴圆P的方程为x2+y2+6x-16=0.
(2)圆P的方程即(x+3)2+y2=25,∴圆心P(-3,0),半径r=5,
圆Q:x2+y2-2ay+a2-4=0,即x2+(y-a)2=4,
圆心Q(0,a),半径r=2,
∵圆P和圆Q相外切,∴|PQ|=5+2=7,
∴(-3-0)2+(0-a)2=72,
解得a=$±2\sqrt{10}$.
点评 本题考查圆的方程的求法,考查实数值的求法,考查直线与圆的位置关系,两点间距离公式的应用等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-4,4) | B. | (-4,4] | C. | (-∞,4) | D. | (-∞,4)∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$-sin2n | B. | sin2n-$\frac{2}{3}$ | C. | $\frac{1}{3}$-cos2n | D. | cos2n+$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{4}$) | B. | ($\frac{5}{12}$,$\frac{3}{4}$] | C. | ($\frac{3}{4}$,1] | D. | ($\frac{3}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
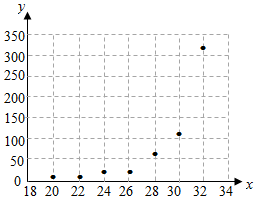 为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型①$y={C_1}{x^2}+{C_2}$与模型;②$y={e^{{C_3}x+{C_4}}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.
为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型①$y={C_1}{x^2}+{C_2}$与模型;②$y={e^{{C_3}x+{C_4}}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.| 温度x/°C | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline x$ | $\overline t$ | $\overline y$ | $\overline z$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{{\sum_{i=1}^7{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({x_i}-\overline x)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({z_i}-\overline z)({x_i}-\overline x)}}}{{\sum_{i=1}^7{{{({x_i}-\overline x)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({z_i}-\overline z)({t_i}-\overline t)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com