
 ����ij��ѧ�Ը���ѧ���������ʲ��ԣ���֪����ij������ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ��ͼ����λ��cm��
����ij��ѧ�Ը���ѧ���������ʲ��ԣ���֪����ij������ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ��ͼ����λ��cm������ ��1���ɾ�Ҷͼ�����Ů��������Զ�ɼ�����λ����
��2�������ɼ����ϸ���8�ˣ������ϸ���4�ˣ��÷ֲ�����ķ�������������гɼ����ϸ�ѧ��Ӧ��ȡ��������
��3���ɣ�2����֪6���У�4�˺ϸ�2�˲��ϸ���ϸ�ѧ��Ϊ a��b��c��d ���ϸ�ѧ��Ϊe��f�������оٷ��������4��������3�˺ϸ�ĸ��ʣ�
��� �⣺��1��Ů��������Զ�ɼ�����λ��Ϊ��
$\frac{185+188}{2}=186.5$��cm����
��2�������ɼ����ϸ���8�ˣ������ϸ���4�ˣ�
�÷ֲ�����ķ��������гɼ����ϸ�ѧ��Ӧ��ȡ6��$\frac{8}{12}=4$���ˣ�����8�֣�
��3���ɣ�2����֪6���У�4�˺ϸ�2�˲��ϸ�
��ϸ�ѧ��Ϊ a��b��c��d ���ϸ�ѧ��Ϊe��f��
����6������ȡ4���У�
abcd abce abcf abde abdf
abef acde acdf acef adef
bcde bcdf bcef bdef cdef
����15�������¼������з��������Ļ����¼�����9����
����4��������3�˺ϸ�ĸ���p=$\frac{9}{15}=\frac{3}{5}$������12�֣�
���� ���⿼����λ����������Ԫ�������ʵ����ǻ����⣬����ʱҪ�������⣬ע�⾥Ҷͼ���ֲ�������ȿ����¼����ʼ��㹫ʽ�ĺ������ã�


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��a����f��c����f��b�� | B�� | f��c����f��b����f��a�� | C�� | f��a����f��b����f��c�� | D�� | f��b����f��c����f��a�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
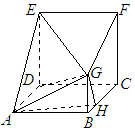 �ڶ�����ABCDEFG�У��ı���ABCD��CDEF�DZ߳���Ϊa�����Σ�CF��ƽ��ABCD��BG��ƽ��ABCD����AB=2BG=4BH
�ڶ�����ABCDEFG�У��ı���ABCD��CDEF�DZ߳���Ϊa�����Σ�CF��ƽ��ABCD��BG��ƽ��ABCD����AB=2BG=4BH�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 36 | C�� | 72 | D�� | 144 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��sin$\frac{��}{8}$����f��cos$\frac{��}{8}$�� | B�� | f��sin1����f��cos1�� | ||
| C�� | f��sin$\frac{��}{12}$����f��sin$\frac{5��}{12}$�� | D�� | f��sin$\frac{��}{12}$����f��tan$\frac{��}{12}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com