
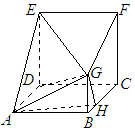
 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH分析 (1)连接FH,由题意,知CD⊥平面BCFG,从而CD⊥GH.再求出GH⊥FG,由此能证明平面AGH⊥平面EFG.
(2)由VG-ADE=VE-ADE,能求出三棱锥G-ADE的体积.
解答 证明:(1)连接FH,由题意,知CD⊥BC,CD⊥CF,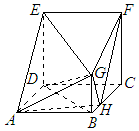
∴CD⊥平面BCFG.
又∵GH?平面BCFG,∴CD⊥GH.
又∵EF∥CD,∴EF⊥GH,…(2分)
由题意,得BH=$\frac{1}{4}a$,CH=$\frac{3}{4}a$,BG=$\frac{1}{2}a$,
∴GH2=BG2+BH2=$\frac{5}{16}{a}^{2}$,
FG2=(CF-BG)2+BC2=$\frac{5}{4}{a}^{2}$,FH2=CF2+CH2=$\frac{25}{16}{a}^{2}$,
则FH2=FG2+GH2,∴GH⊥FG.…(4分)
又∵EF∩FG=F,GH⊥平面EFG.…(5分)
∵GH?平面AGH,∴平面AGH⊥平面EFG.…(6分)
解:(2)∵CF⊥平面ABCD,BG⊥平面ABCD,∴CF∥BG,
又∵ED∥CF,∴BG∥ED,
∴BG∥平面ADE,∴VG-ADE=VE-ADE,
∵AB∥CD,∴AB⊥平面ADE,
∴三棱锥G-ADE的体积VG-ADE=VE-ADE=$\frac{1}{3}×\frac{1}{2}×4×4×4=\frac{32}{3}$.
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪[2,3) | B. | (-∞,0]∪(2,3) | C. | [0,2) | D. | [0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 怀化某中学对高三学生进行体质测试,已知高三某个班有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm)
怀化某中学对高三学生进行体质测试,已知高三某个班有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com