
分析 (1)由解析式列出不等式,由指数的运算性质求出函数的定义域,由指数函数的性质求出值域;
(2)由解析式化简f(x)≤1,利用对数函数的性质求出不等式的解集.
解答 解:(1)由题意得,4-8x≥0,
则23x≤22,即3x≤2,解得x≤$\frac{2}{3}$,
所以函数f(x)的定义域是(-∞,$\frac{2}{3}$];
又4-8x<4,所以$0≤\sqrt{4-{8^x}}<2$,
即函数f(x)的值域为[0,2).
(2)由f(x)≤1得,$\sqrt{4-{8^x}}≤1$,
则0≤4-8x≤1,即3≤8x≤4,
两边取以8为底的对数,解得${log_8}3≤x≤\frac{2}{3}$,
所以不等式的解集是$[lo{g}_{8}3,\frac{2}{3}]$.
点评 本题考查了指数不等式的解法,指数运算性质,函数的定义域,以及对数、指数函数的性质,属于中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{5π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1] | B. | [1,2] | C. | [-1,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(c)<f(b) | B. | f(c)<f(b)<f(a) | C. | f(a)<f(b)<f(c) | D. | f(b)<f(c)<f(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
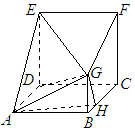 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com