
分析 根据命题的否定的定义可知①错误;通过原命题和逆否命题的同真同假,结合充要条件的判断方法可知②正确;由于逆否命题为真,所以原命题也为真,故③正确;根据零点的定义可知④错误.
解答 解:对于①:根据命题的否定的定义,¬p:?x∈R,x2+x-1≥0,故①错误;
对于②:∵p是q的必要不充分条件,∴若p则q为假,若q则p为真.
∵原命题与逆否命题是等价命题,∴由¬q则¬p为假,若¬p则¬q为真.
因此,¬p是¬q的充分不必要条件.故②正确;
对于③:逆否命题为“若x=y,则sinx=siny“,易知逆否命题为真,而原命题和逆否命题的同真同假,所以原命题为真命题,故③正确;
对于④:函数的零点是指函数图象与x轴交点的横坐标,所以该函数的零点是x=1,而不是(1,0),故④错误.
故答案为:②③.
点评 本题主要考查了命题的否定,充分必要条件,四种命题的真假性判断以及函数零点的定义等基本概念.


科目:高中数学 来源: 题型:选择题
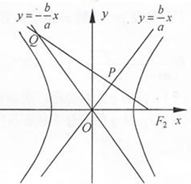 过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦点F2向其一条渐近线作垂线l,垂足为P,l与另一条渐近线交于Q点,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,则双曲线的离心率为( )
过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的右焦点F2向其一条渐近线作垂线l,垂足为P,l与另一条渐近线交于Q点,若$\overrightarrow{Q{F}_{2}}$=3$\overrightarrow{P{F}_{2}}$,则双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1} | B. | {x|x<0} | C. | {x|x>0} | D. | {x|x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 8 | C. | 4 | D. | -8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com