
【题目】已知函数f(x)=a1nx﹣ax+1(a∈R且a≠0).
(1)求函数f(x)的单调区间;
(2)求证:![]() (n≥2,n∈N*).
(n≥2,n∈N*).
【答案】(1)当a>0时, f(x)的单调递增区间(0,1),单调递减区间(1,+∞);
当a<0时, f(x)的单调递减区间(0,1),单调递增区间(1,+∞);
(2)证明,见解析
【解析】
(1)对f(x)求导,分a>0,a<0两种情况讨论,分析函数单调性即可;
(2)令a=1,由(1)可证得lnx<x﹣1,即![]() ,叠乘可得证.
,叠乘可得证.
(1)∵f(x)=a1nx﹣ax+1,∴f′(x)![]() a
a![]() ,
,
①当a>0时,
若0<x<1,则f′(x)>0,若x>1,f′(x)<0,
∴f(x)的单调递增区间(0,1),单调递减区间(1,+∞);
②当a<0时,
若0<x<1,则f′(x)<0,若x>1,f′(x)>0,
∴f(x)的单调递减区间(0,1),单调递增区间(1,+∞);
(2)令a=1,则f(x)=lnx﹣x+1,所以f(1)=0,
由(1)可知f(x)在[1,+∞)单调递减,
故f(x)≤f(1),(当x=1时取等号),
所以lnx﹣x+1<0,即lnx<x﹣1,
从而有0<lnn<n﹣1,(n≥2,n∈N*),
即![]() (n≥2,n∈N*),
(n≥2,n∈N*),
∴![]() (n≥2,n∈N*).
(n≥2,n∈N*).


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知极点与平面直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,直线
轴的正半轴重合,直线![]() 的参数方程为
的参数方程为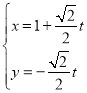 (
(![]() 是参数),曲线
是参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() 上一点,求使
上一点,求使![]() 面积取得最大值时的
面积取得最大值时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 后,与曲线
后,与曲线![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的广告支出![]() (单位:万元)与销售收入
(单位:万元)与销售收入![]() (单位:万元)之间有下表所对应的数据:
(单位:万元)之间有下表所对应的数据:
广告支出 | 1 | 2 | 3 | 4 |
销售收入 | 12 | 28 | 42 | 56 |
(1)画出表中数据的散点图;
(2)求出![]() 对
对![]() 的线性回归方程;
的线性回归方程;
(3)若广告费为9万元,则销售收入约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
,![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
,![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com