
分析 (1)当a=3时,化简f(x)=$\frac{3}{x}$+|lnx-3|=$\frac{3}{x}$-lnx+3,x∈[1,e2];从而求导,再求切线方程;
(2)由题意得,$\frac{a}{x}$+|lnx-a|≤$\frac{3}{2}$,分a≥2与0<a<2讨论求函数的最值,从而化恒成立问题为最值问题即可.
解答 解:(1)当a=3时,f(x)=$\frac{3}{x}$+|lnx-3|=$\frac{3}{x}$-lnx+3,x∈[1,e2];
故f(3)=1-ln3+3=4-ln3,
f′(x)=-$\frac{3}{{x}^{2}}$-$\frac{1}{x}$,f′(3)=-$\frac{1}{3}$-$\frac{1}{3}$=-$\frac{2}{3}$;
故曲线y=f(x)在点(3,f(3))处的切线方程为y-(4-ln3)=-$\frac{2}{3}$(x-3),
即2x+3y-18+3ln3=0.
(2)由题意得,$\frac{a}{x}$+|lnx-a|≤$\frac{3}{2}$,
当a≥2时,上式可化为$\frac{a}{x}$-lnx+a≤$\frac{3}{2}$恒成立,
且$\frac{a}{x}$-lnx+a在[1,e2]上是减函数,
故只需使a+a≤$\frac{3}{2}$,无解;
当0<a<2时,
f(x)=$\left\{\begin{array}{l}{\frac{a}{x}+lnx-a,x∈[{e}^{a},{e}^{2}]}\\{\frac{a}{x}-lnx+a,x∈[1,{e}^{a}]}\end{array}\right.$,
故f(x)在[1,ea]上是减函数,在[ea,e2]上是增函数,
故只需使$\left\{\begin{array}{l}{a+a≤\frac{3}{2}}\\{\frac{a}{{e}^{2}}+2-a≤\frac{3}{2}}\end{array}\right.$;
解得$\frac{{e}^{2}}{2({e}^{2}-1)}$≤a≤$\frac{3}{4}$.
点评 本题考查了导数的综合应用及恒成立问题,考查学生分析解决问题的能力,考查分类讨论的数学思想,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
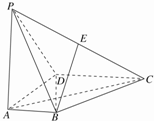 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
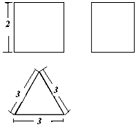 一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是( )
一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是( )| A. | 16π | B. | 12π | C. | 8π | D. | 25π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com