
分析 (1)由已知条件可知|PD|与点P到直线y=-$\frac{1}{2}$的距离之间的关系,进而得出点M到直线y=-1的距离等于它到点C(0,1)的距离,由抛物线定义,求得圆心P的轨迹C的方程;
(2)先利用条件设出圆的方程,并求出A、B两点的坐标以及|MA|=d1,|MB|=d2的表达式,代入$\frac{{d}_{1}}{{d}_{2}}$+$\frac{{d}_{2}}{{d}_{1}}$,整理后利用基本不等式求最大值即可.
解答 解:(1)设动圆P的半径为r,
动圆P与圆D:x2+(y-1)2=$\frac{1}{4}$外切.
∴|PD|=r+$\frac{1}{2}$,
动圆P与直线l:y=-$\frac{1}{2}$相切,
∴点P到直线y=-$\frac{1}{2}$的距离为r,
则点P到直线y=-1为r+$\frac{1}{2}$,
则动点P到直线y=-1的距离等于它到点D(0,1)的距离,
∴点M的轨迹是抛物线,
∴圆心P的轨迹方程为x2=4y;
(2)设圆Q的圆心坐标为Q(a,b),则a2=4b.①
圆Q的半径为|MQ|=$\sqrt{{a}^{2}+(b-2)^{2}}$,
圆Q的方程为(x-a)2+(y-b)2=a2+(b-2)2.
令y=0,则(x-a)2+b2=a2+(b-2)2,
整理得,x2-2ax+4b-4=0.②
由①、②解得,x=a±2.
不妨设A(a-2,0),B(a+2,0),
∴d1=$\sqrt{(a-2)^{2}+4}$,d2=$\sqrt{(a+2)^{2}+4}$,
∴$\frac{{d}_{1}}{{d}_{2}}$+$\frac{{d}_{2}}{{d}_{1}}$=$\frac{2{a}^{2}+16}{\sqrt{{a}^{4}+64}}$=$\sqrt{1+\frac{16{a}^{2}}{{a}^{4}+64}}$,③
当a≠0时,由③得$\frac{{d}_{1}}{{d}_{2}}$+$\frac{{d}_{2}}{{d}_{1}}$=$\sqrt{1+\frac{16{a}^{2}}{{a}^{4}+64}}$≤2$\sqrt{2}$.
当且仅当a=±2$\sqrt{2}$时,等号成立.
当a=0时,由③得,$\sqrt{1+\frac{16{a}^{2}}{{a}^{4}+64}}$=2.
故当a=±2$\sqrt{2}$时,$\sqrt{1+\frac{16{a}^{2}}{{a}^{4}+64}}$的最大值为2$\sqrt{2}$.
点评 本题考查求抛物线的轨迹方程,考查点的轨迹方程的求法,均值不等式的应用,解题时要认真审题,注意直线和圆锥曲线的位置关系的灵活运用,属于中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量 | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
| 频率 | 0.2 | a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
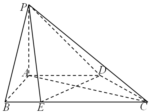 如图,在四棱锥P-ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
如图,在四棱锥P-ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 2f(3)<3f(2) | C. | 3f(4)<4f(3) | D. | 2f(3)<3f(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com