
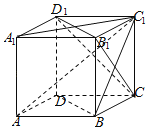
【题目】如图,在正方体ABCD-A1B1C1D1中,有下面结论:

①AC∥平面CB1D1;
②AC1⊥平面CB1D1;
③AC1与底面ABCD所成角的正切值是![]() ;
;
④AD1与BD为异面直线.其中正确的结论的序号是________.
【答案】②③④
【解析】
利用线面平行,线面垂直和线面所成角的定义分别判断.①因为AC∩平面CB1D1=C,所以AC∥平面CB1D1错误;根据线面垂直的判定定理得到②正确;由线面角的定义得到AC1在底面ABCD的射影为AC,所以∠C1AC是AC1与底面ABCD所成的角,在三角形中求得正切值③正确;由异面直线的定义可知,AD1与BD为异面直线,所以④正确.
①因为AC∩平面CB1D1=C,所以AC∥平面CB1D1错误,所以①错误.
②连结BC1,A1 C1,则BC1⊥B1 C,又因为AB⊥面BC C1B1
故 AB⊥B1 C, AB∩BC1=B,故B1 C⊥面ABC1
进而得到AC1⊥B1C,
连接A1 C1,同理可证B1D1⊥AC1
又因为B1D1∩B1 C于点B1
故得到AC1⊥平面CB1D1
所以②正确.
③因为AC1在底面ABCD的射影为AC,所以∠C1AC是AC1与底面ABCD所成的角,设正方体的边长为a,则AC=![]()
所以![]() 所以③正确.
所以③正确.
④由异面直线的定义可知,AD1与BD为异面直线,所以④正确.
故答案为:②③④.


科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
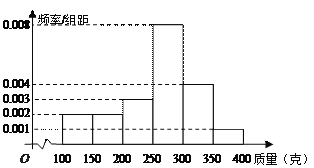
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a、b、c,已知a=csinB+bcosC.
(1)求A+C的值;
(2)若b= ![]() ,求△ABC面积的最值.
,求△ABC面积的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 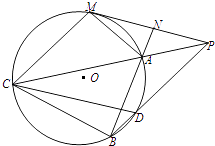
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}满足b3=3,b5=9.
(1)分别求数列{an},{bn}的通项公式;
(2)设Cn= ![]() (n∈N*),求证Cn+1<Cn
(n∈N*),求证Cn+1<Cn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=﹣sin(ωx+φ)(ω>0,φ∈(﹣ ![]() ,
, ![]() ))的一条对称轴为x=
))的一条对称轴为x= ![]() ,一个对称中心为(
,一个对称中心为( ![]() ,0),在区间[0,
,0),在区间[0, ![]() ]上单调.
]上单调.
(1)求ω,φ的值;
(2)用描点法作出y=sin(ωx+φ)在[0,π]上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax-![]() x2-3ln x,其中a∈R,为常数.
x2-3ln x,其中a∈R,为常数.
(1)若f(x)在x∈[1,+∞)上是减函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com