
已知函数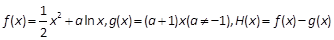 。
。
(1)若 的单调减区间是
的单调减区间是 ,求实数a的值;
,求实数a的值;
(2)若函数 在区间
在区间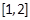 上都为单调函数且它们的单调性相同,求实数a的取值范围;
上都为单调函数且它们的单调性相同,求实数a的取值范围;
(3)a、b是函数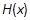 的两个极值点,a<b,
的两个极值点,a<b,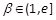 。求证:对任意的
。求证:对任意的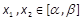 ,不等式
,不等式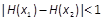 成立.
成立.
(1)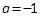 (2)
(2) 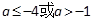 (3)略
(3)略
解析试题分析:(1)由题得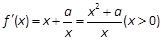 ,以及
,以及 的单调减区间,解得
的单调减区间,解得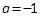 ;
;
(2)函数 在区间
在区间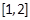 上都为单调函数且它们的单调性相同,转化为不等式恒成立的问题.
上都为单调函数且它们的单调性相同,转化为不等式恒成立的问题.
(3)由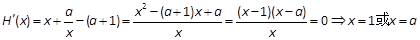
又∵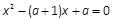 有两个不相等的正跟a,b且a<b,
有两个不相等的正跟a,b且a<b, 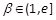 ,得
,得 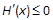 , 即
, 即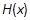 在
在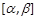 上单调递减,
上单调递减,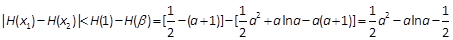
设 , 求得
, 求得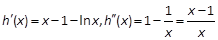 再利用单调性即可.
再利用单调性即可.
(1) 由题得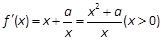 ,
,
要使 的单调减区间是
的单调减区间是 则
则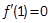 ,解得
,解得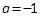 ; (2分)
; (2分)
另一方面当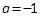 时
时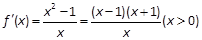 ,
,
由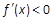 解得
解得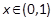 ,即
,即 的单调减区间是
的单调减区间是 .
.
综上所述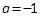 . (4分)
. (4分)
(2)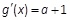 , 函数
, 函数 在区间
在区间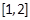 上都为单调函数且它们的单调性相同,
上都为单调函数且它们的单调性相同,
∴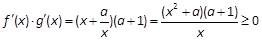 , ∴
, ∴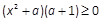 (6分)
(6分)
∵ ,又
,又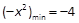
∴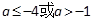 (8分)
(8分)
(3)∵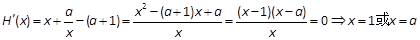
又∵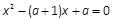 有两个不相等的正跟a,b且a<b,
有两个不相等的正跟a,b且a<b, 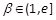 ,∴
,∴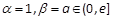
∴当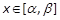 时,
时, 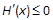 , 即
, 即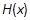 在
在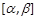 上单调递减,∴
上单调递减,∴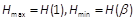 (10分)
(10分)
则对任意的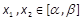 ,
,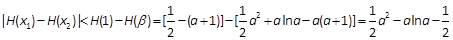
设 , 则
, 则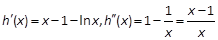
当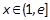 时
时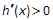 , ∴
, ∴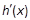 在
在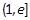 上单增, ∴
上单增, ∴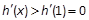 , ∴
, ∴ 也在
也在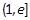 上单增, (12分)
上单增, (12分)
∴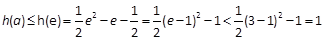
∴不等式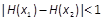 对任意的
对任意的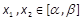 成立. (14分)
成立. (14分)
考点:利用导数求单调区间以及参数的取值范围;不等式恒成立的问题;利用导数求极值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
对于三次函数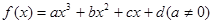 ,定义
,定义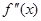 是
是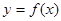 的导函数
的导函数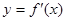 的导函数,若方程
的导函数,若方程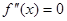 有实数解
有实数解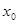 ,则称点
,则称点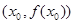 为函数
为函数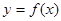 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数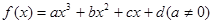 都关于点
都关于点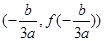 对称:
对称:
②存在三次函数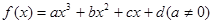 ,若
,若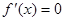 有实数解
有实数解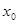 ,则点
,则点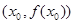 为函数
为函数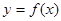 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数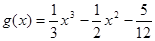 ,则:
,则: 
其中所有正确结论的序号是( ).
| A.①②④ | B.①②③ | C.①③④ | D.②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知二次函数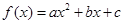 的图像过点
的图像过点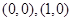 和
和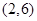 ,直线
,直线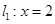 ,直线
,直线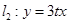 (其中
(其中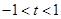 ,
,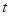 为常数);若直线
为常数);若直线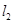 与函数
与函数 的图像以及直线
的图像以及直线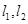 与函数
与函数 以及的图像所围成的封闭图形如阴影所示.
以及的图像所围成的封闭图形如阴影所示.
(1)求 ;
;
(2)求阴影面积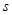 关于
关于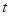 的函数
的函数 的解析式;
的解析式;
(3)若过点 可作曲线
可作曲线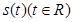 的三条切线,求实数
的三条切线,求实数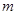 的取值范围.
的取值范围.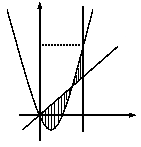
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com