
(本题满分14分)
如图1,直角梯形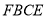 中, 四边形
中, 四边形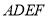 是正方形,
是正方形,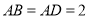 ,
,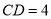 .将正方形沿
.将正方形沿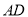 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面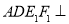 面
面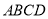 ,
,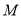 是
是 中点.
中点.
(1) 证明: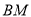 ∥平面
∥平面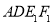 ;
;
(2) 求三棱锥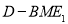 的体积.
的体积.


图1 图2
(1)证明过程详见解析;(2)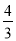 .
.
【解析】
试题分析:本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,作出辅助线MN,N为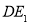 中点,在
中点,在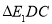 中,利用中位线得到
中,利用中位线得到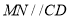 ,且
,且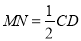 ,结合已知条件,可证出四边形ABMN为平行四边形,所以
,结合已知条件,可证出四边形ABMN为平行四边形,所以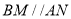 ,利用线面平行的判定,得
,利用线面平行的判定,得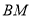 ∥平面
∥平面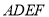 ;第二问,利用面面垂直的性质,判断
;第二问,利用面面垂直的性质,判断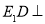 面
面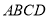 ,再利用已知的边长,可证出
,再利用已知的边长,可证出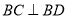 ,则利用线面垂直的判定得
,则利用线面垂直的判定得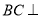 平面BDE,再利用面面垂直的判定得平面
平面BDE,再利用面面垂直的判定得平面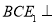 平面
平面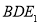 ,所以作
,所以作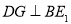 ,则利用面面垂直的性质,可得
,则利用面面垂直的性质,可得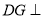 平面
平面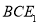 ,则
,则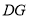 为三棱锥的高,再利用三棱锥的体积公式求体积即可.
为三棱锥的高,再利用三棱锥的体积公式求体积即可.
(1)证明:取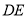 中点
中点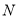 ,连结
,连结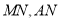 .
.

在△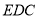 中,
中,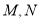 分别为
分别为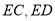 的中点,所以
的中点,所以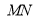 ∥
∥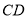
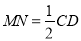 .由已知
.由已知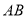 ∥
∥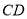 ,
,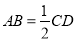 ,所以
,所以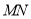 ∥
∥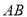 ,且
,且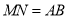 .所以四边形
.所以四边形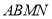 为平行四边形,所以
为平行四边形,所以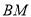 ∥
∥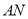 . 3分
. 3分
又因为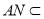 平面
平面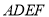 ,且
,且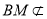 平面
平面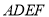 ,
,
所以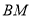 ∥平面
∥平面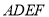 . 4分
. 4分
(2)面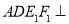 面
面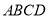 ,
,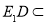 面
面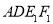 ,
,
面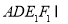 面
面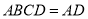 ,
,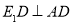 ,
,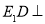 面
面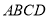
又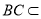 面
面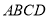 ,
,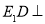
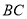 6分
6分
梯形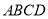 中,
中,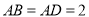 ,
,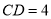 ,
,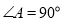 ,
,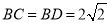
所以,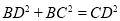 ,
, 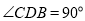 ,
,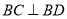
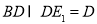 ,所以,
,所以, 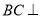 平面
平面 8分
8分
又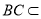 平面
平面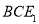 ,所以,平面
,所以,平面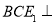 平面
平面
作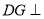
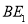 ,则
,则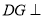 平面
平面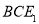 ,
,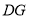 是所求三棱锥高 10分
是所求三棱锥高 10分
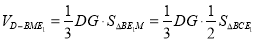
在直角三角形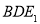 中,由面积关系可得
中,由面积关系可得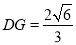 ,又
,又 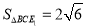
所以,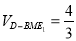 14分
14分
另【解析】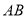 ∥
∥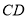 ,
,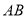
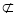 面
面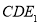 ,
,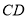
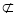 面
面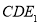 ,
,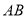 ∥平面
∥平面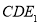 ,
,
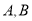 两点到平面
两点到平面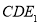 距离相等 7分
距离相等 7分
因为翻折后垂直关系不变,所以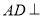 平面
平面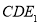 ,
,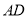 是三棱锥
是三棱锥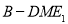 高 9分
高 9分
面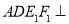 面
面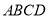 ,
,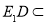 面
面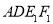 ,面
,面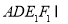 面
面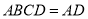 ,
,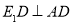 ,
,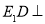 面
面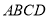 ,
,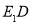
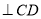 ,
, 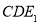 是直角三角形 11分
是直角三角形 11分
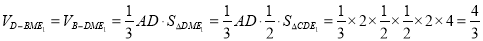 14分
14分
考点:中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、三棱锥的体积.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试文科数学试卷(解析版) 题型:解答题
各项均为正数的数列{an}中,设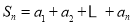 ,
,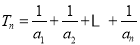 ,且
,且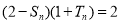 ,
,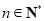 .
.
(1)设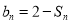 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设 ,求集合
,求集合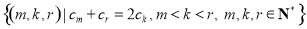 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)文科数学试卷(解析版) 题型:填空题
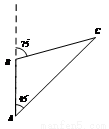
一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是__________海里.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)文科数学试卷(解析版) 题型:选择题
由于工业化城镇化的推进,大气污染日益加重,空气质量逐步恶化,雾霾天气频率增大,大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如下列联表:问有多大的把握认为是否患心脏病与性别有关. 答:.
A.95% B.99% C.99.5% D.99.9%
| 患心脏病 | 不患心脏病 | 合计 |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
参考临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: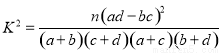 其中n = a + b + c + d).
其中n = a + b + c + d).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二理科数学试卷(解析版) 题型:填空题
某小区有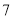 个连在一起的车位,现有
个连在一起的车位,现有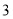 辆不同型号的车需要停放,如果要求剩余的
辆不同型号的车需要停放,如果要求剩余的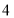 个车位连在一起,那么不同的停放方法共有 __________种.(用数字作答)
个车位连在一起,那么不同的停放方法共有 __________种.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com