考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①,易知BC1∥平面AD1,BC1上任意一点到平面AD1C的距离相等,三棱锥A-D1PC的体积不变,可判断①;
②,当P在直线BC1上运动时,直线AB与平面ACD1所成角和直线AC1与平面ACD1所成角不相等,可判断②.
③,当P在直线BC1上运动时,易知AP的轨迹是平面PAD1,可判断③.
④,平面A1B1C1D1上的直线D1A1,符合题意,可判断④.
解答:
解:①∵BC1∥AD1,BC1?平面AD1C,AD1?平面AD1C,
∴BC1∥平面AD1C,BC1上任意一点到平面AD1C的距离相等,
∴VA-D1PC=VP-D1AC=VB-D1AC,为定值,即点P在直线BC1上运动时,三棱锥A-D1PC的体积不变,故①正确;
②P在直线BC1上运动时,直线AB与平面ACD1所成角和直线AC1与平面ACD1所成角不相等,故②不正确.
③当P在直线BC1上运动时,AP的轨迹是平面ABC1,即平面PAD1,即二面角P-AD1-C的大小不受影响,故③正确.
④∵M是平面A1B1C1D1上到点D和C1距离相等的点,而DD1=C1D1,
∴M点的轨迹是直线D1A1,故④正确.
综上所述,真命题为①③④,共3个,
故答案为:3.
点评:本题考查空间正方体中线面角、二面角的概念及应用,着重考查空间想象能力与推理运算能力,属于中档题.

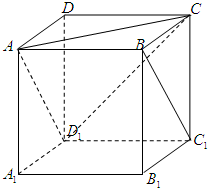 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题:

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案