
【题目】已知下面四个命题:
①“若![]() ,则
,则![]() 或
或![]() ”的逆否命题为“若
”的逆否命题为“若![]() 且
且![]() ,则
,则![]() ”
”
②命题:“![]() ,若
,若![]() ,则
,则![]() ”,用反证法证明时应假设
”,用反证法证明时应假设![]() 或
或![]() .
.
③命题![]() 存在
存在![]() ,使得
,使得![]() ,则
,则![]() :任意
:任意![]() ,都有
,都有![]()
④若![]() 且
且![]() 为假命题,则
为假命题,则![]() 均为假命题,其中真命题个数为( )
均为假命题,其中真命题个数为( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】直角坐标系![]() 中,圆
中,圆![]()
![]() (
(![]() 为参数)上的每一点的横坐标不变,纵坐标变为原来的
为参数)上的每一点的横坐标不变,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与两坐标轴分别相交于
与两坐标轴分别相交于![]() 两点,点
两点,点![]() 在
在![]() 上,求
上,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x的焦点为F,准线为l,过l上一点P作抛物线C的两条切线,切点为A,B.
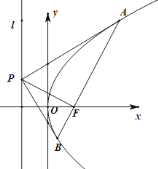
(1)求证:直线AB过焦点F;
(2)若|PA|=8,|PB|=6,求|PF|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,若△
,若△![]() 的三个顶点都在抛物线
的三个顶点都在抛物线![]() 上,且
上,且![]() ,则称该三角形为“核心三角形”.
,则称该三角形为“核心三角形”.
(1)是否存在“核心三角形”,其中两个顶点的坐标分别为![]() 和
和![]() ?请说明理由;
?请说明理由;
(2)设“核心三角形”![]() 的一边
的一边![]() 所在直线的斜率为4,求直线
所在直线的斜率为4,求直线![]() 的方程;
的方程;
(3)已知△![]() 是“核心三角形”,证明:点
是“核心三角形”,证明:点![]() 的横坐标小于2.
的横坐标小于2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列![]() 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使数列
,使数列![]() 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(comsummer priceindex)的简称.居民消费价格指数是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.如图是根据国家统计局发布的2019年4月——2020年4月我国CPI涨跌幅数据绘制的折线图(注:2019年6月与2018年6月相比较,叫同比;2019年6月与2019年5月相比较,叫环比),根据该折线图,则下列结论正确的是( )
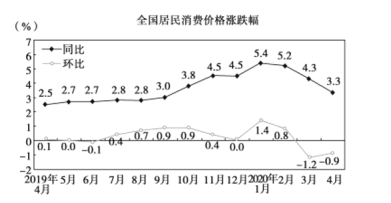
A.2019年4月至2020年4月各月与去年同期比较,CPI有涨有跌
B.2019年4月居民消费价格同比涨幅最小,2020年1月同比涨幅最大
C.2020年1月至2020年4月CPI只跌不涨
D.2019年4月至2019年6月CPI涨跌波动不大,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com