
分析 ①根据函数成立的条件进行求解即可.
②根据函数奇偶性的定义进行判断,
③根据函数与方程之间的关系进行求解判断,
④根据复合函数单调性的性质进行判断,
⑤根据函数单调性以及对数函数的值域的性质进行求解.
解答 解:①要使函数有意义,则$\left\{\begin{array}{l}{3-2x>0}\\{lo{g}_{\frac{1}{2}}(3-2x)≥0}\end{array}\right.$,即0<3-2x≤1,得1≤x<$\frac{3}{2}$,即函数y=$\sqrt{lo{g}_{\frac{1}{2}}(3-2x)}$的定义域是[1,$\frac{3}{2}$);故①错误,
②函数的定义域为(-∞,+∞),∵f(x)=log2($\sqrt{{x}^{2}+1}$-x),
∴f(-x)+f(x)=log2($\sqrt{{x}^{2}+1}$+x)+log2($\sqrt{{x}^{2}+1}$-x)=log2($\sqrt{{x}^{2}+1}$+x)($\sqrt{{x}^{2}+1}$-x)=log2(x2+1-x2)=log21=0,
即f(-x)=-f(x),则f(x)为奇函数;故②正确,
③已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x(x≤0)}\\{{x}^{-\frac{1}{2}}(x>0)}\end{array}\right.$,若函数g(x)=f(x)+m有3个零点,
则f(x)+m=0,得-m=f(x),
作出函数f(x)的图象如图:
要使两个函数有三个交点,
则0<-m<1,即-1<m<0,
即实数m的取值范围是(-1,0);故③正确,
④函数y=loga(5-ax)在区间[-1,3)上单调递减,则$\left\{\begin{array}{l}{a>1}\\{5-3a≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a>1}\\{a≤\frac{5}{3}}\end{array}\right.$,即1<a≤$\frac{5}{3}$,
即a的范围是(1,$\frac{5}{3}$];故④正确,
⑤若函数y=($\frac{2}{2c+1}$)-x=($\frac{2c+1}{2}$)x在R上单调递减,
则0<$\frac{2c+1}{2}$<1得-$\frac{1}{2}$<c<$\frac{1}{2}$,
∵函数g(x)=lg(2cx2+2x+1)的值域为R,
∴若c=0,则g(x)=lg(2x+1)的值域为R,满足条件.
若c≠0,
则等价为$\left\{\begin{array}{l}{2c>0}\\{△=4-4c≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{c>0}\\{c≤1}\end{array}\right.$,得0<c≤1,
综上0<c<$\frac{1}{2}$,
则c的取值范围是(0,$\frac{1}{2}$).故⑤正确,
故答案为:②③④⑤.
点评 本题主要考查命题的真假判断,涉及函数的性质,考查学生的综合应用能力,有一定的难度.


科目:高中数学 来源: 题型:解答题
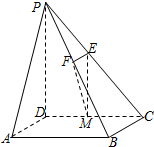 如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧棱PD⊥底面ABCD,E,F,M分别是PC,PB,CD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧棱PD⊥底面ABCD,E,F,M分别是PC,PB,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 读营养说明 | 不读营养说明 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 12 | 20 |
| 合计 | 24 | 16 | 40 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com