
分析 对5个命题分别进行判断,即可得出结论.
解答 解:①一个底面半径为1,母线长为2的圆锥的表面积为π+$\frac{1}{2}×2π×2$=3π,正确;
②函数f(x)=sinx-2cosx=$\sqrt{5}$sin(x-α)(其中cosα=$\frac{\sqrt{5}}{5}$,sinα=$\frac{2\sqrt{5}}{5}$),
∵x=θ时,函数f(x)取得最大值,∴sin(θ-α)=1,即sinθ-2cosθ=$\sqrt{5}$,
又sin2θ+cos2θ=1,联立得(2cosθ+$\sqrt{5}$)2+cos2θ=1,解得cosθ=-$\frac{2\sqrt{5}}{5}$,正确;
③由已知得,a1<0,d>0,a10<0,a11>0,∴a1+a19<0,a10+a11>0,∴a1+a20>0,
∴S19<0,S20>0,故n=20,不正确;
④画出y=|lgx|的图象如图:
∵0<m<n,且f(m)=f(n),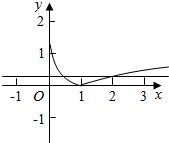
∴0<m<1,n>1
∴-lgm=lgn,
∴mn=1,
即n=$\frac{1}{m}$,
∴m+2n=m+$\frac{2}{m}$.
∵函数g(m)=m+$\frac{2}{m}$在(0,1)上单调递减,
∴g(m)>g(1)=1+2=3,
即m+2n>3,则m+2n的取值范围是(3,+∞),不正确;
⑤∵O为AB的中点,∴$\overrightarrow{PA}$+$\overrightarrow{PB}$=2$\overrightarrow{PO}$,
∴($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$=2$\overrightarrow{PO}$•$\overrightarrow{PC}$=-2|$\overrightarrow{PO}$||$\overrightarrow{PC}$|;
又|$\overrightarrow{PO}$|+|$\overrightarrow{PC}$|=2|$\overrightarrow{OC}$|=2为定值,
∴当且仅当|$\overrightarrow{PO}$|=|$\overrightarrow{PC}$|=1,即P为OC的中点时,($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是-2,正确;
故答案为:①②④.
点评 本题考查命题的真假判断,考查学生分析解决问题的能力,知识综合性强,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{8}$ | B. | $\frac{15}{4}$ | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com